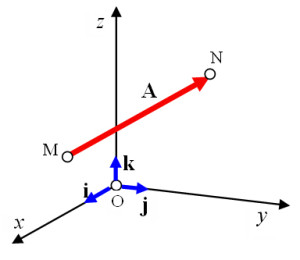
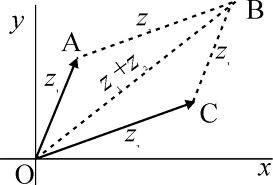
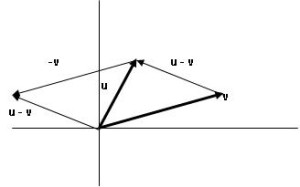
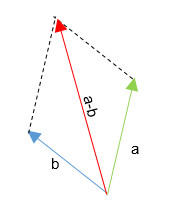
Un vector es un segmento de recta que tiene magnitud, sentido y dirección.
Para calcular su magnitud se hace de la siguiente manera:
|V|=√x^2 +y^2
Es decir, la raíz cuadrada de la suma de los cuadrados de las mediciones del vector nos da la magnitud de éste.
Para calcular su dirección, es decir el ángulo del vector se hace de la siguiente manera:
Θ=Tan^-1 y/x
Es decir, la dirección es la tangente a la menos 1 de la división de la medición de y sobre la medición de x.
Esto es solo para vectores sencillos, cuando se te presentan dos vectores varían un poco las maneras de calcular la magnitud y la dirección.
La magnitud se calcula de la siguiente manera:
|V|= √[(x2-x1)^2 +(y2-y1)^2]
Es decir, la magnitud ahora sera la raíz cuadrada de la resta de las mediciones de x2 menos x1 mas la resta de las mediciones de y2 menos y1.
Y la dirección sera así:
Θ=Tan^-1 yz-y1/x2-x1
Es decir, la tangente a la menos 1 de la division de la resta de y2 menos y1 sobre la resta de x2 menos x1.
A continuación unos ejemplos:
1. Calcular magnitud y dirección del siguiente vector:
V(3,7)
El 3 es X y 7 es Y.
SIEMPRE el numero de la izquierda sera X y el de la derecha Y.
Entonces su magnitud es:
|V|=√3^2 + 7^2 = √58
*Para evitar el uso de decimales, cuando la raíz no es exacta la dejamos expresada.
Y la dirección de este vector seria:
Θ=Tan^-1 (7/3) = 66.8
*El resultado de la dirección siempre sera en grados.
Ahora un ejemplo con dos vectores:
- U(3,2)
V(4,1)
Su magnitud sería:
|V|=√4-3^2 + 1-2^2 = √2
Y su dirección:
Θ=Tan^-1 (4-3/1-2) = -45 = 360 – 45 = 315
*Cuando sale de la operación el ángulo negative se le suma 360 y el resultado es la dirección del vector.
Esa es la manera de calcular el sentido y la dirección en vectores, ya sea de uno o de dos, ahora vienen las operaciones de vectores que son la suma, la resta y la multiplicación.
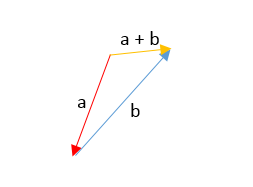
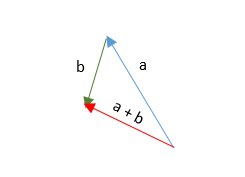
Suma de Vectores:
Para sumar vectores es sencillo, con los dos que tienes sean U(X1,Y1) y V(X2,Y2), se suman sus correspondientes, es decir el vector U+V seria igual a [(X1+X2), (Y1+Y2)]
Ya con el vector resultante, es decir la suma, para conocer su magnitud y dirección es de la misma manera ya vista de cuando se tiene un vector, se hace del vector resultante.
A continuación unos ejemplos para dejar mas clara la suma:
1. Sumar los vectores y encontrar la magnitud y dirección del vector resultante.
U(3,2) V(4,5)
U+V=(3+4),(2+5)=(7,7)
Su magnitud:
|U+V|= √7^2 + 7^2 = √98 = 7√2
Dirección del vector resultante:
Θ=Tan^-1 (7/7) = 45
Así es como fuera un ejemplo de suma de vectores y sacar su magnitud y dirección, así como también te pueden pedir un ejercicio completo también necesites sacar la dirección y magnitude de cada vector como veremos a continuación.
2. Sumar los vectores y sacar la magnitud y dirección del vector resultante y los dos vectores.
U(2,2) V(4,6)
U+V=(2+4),(2+6)=(6,8)
Magnitudes:
|U| = √2^2 + 2^2 = √8
|V| = √4^2 + 6^2 = √52
|U+V|=√6^2 + 8^2 = √100 = 10
Direcciones de los vectores:
ΘU =Tan^-1 (2/2) = 45
Θ=Tan^-1 (6/4) = 56.3
Θ=Tan^-1 (8/6) = 53.13
Esto es suma de vectores ahora prosigamos con algo muy similar a la suma como lo es la resta de vectores.
Resta de Vectores
Así como la suma la resta es muy parecida, lo único diferente es que en igual de sumar restaremos los valores por sus correspondientes, es decir, teniendo U(X1,Y1) y V(X2,Y2) U-V seria (X1-X2),(Y1-Y2) y V-U seria (X2-X1),(Y2-Y1), ojo aquí si es diferente el orden de los vectores pues afecta al vector resultante no como en la suma que era igual como estuvieran acomodados.
Aquí un ejemplo para que quede claro:
1. Restar los vectores y sacar los vectores resultantes posibles.
U=(3,7,5) V=(2,4,8)
U-V = (3-2, 7-4, 5-8) = (1,3,-3)
V-U = (2-3, 4-7, 8-5) = (-1,-3,3)
Ahora vamos a otro ejemplo mas completo sacando la magnitud de ambos vectores resultantes del ejemplo anterior.
2. Retomando los vectores resultantes del ejemplo anterior calcula la magnitud de cada vector.
|U-V|=√1^2 + 3^2 + 3^2 = √19
*La magnitud sera la misma de ambos vectores resultantes pues son los mismos datos únicamente diferente signo y al estar elevados al cuadrado el signo no afecta al producto final.
Es igual que la suma se puede hacer tanto sacar como la magnitud y dirección del vector resultante así como de los vectores dados.
A continuación mas ejercicios para resolver con suma y resta y encontrando la dirección y magnitud de los vectores:
1) Sumar los vectores dados y encontrar su magnitud y dirección así como la de los vectores dados
a) U=(2,4) V=(5,8)
b) U=(1,5) V=(3,9)
2) Restar los vectores dados y encontrar su magnitud y dirección así como la de los vectores dados.
a) U=(1,4) V=(4,10)
b) U=(2,1) V=(7,7)