La finalidad de primero entender bien el método Gauss fue para que cuando se presentaran ecuaciones lineales las pudiéramos resolver pasándolas a matriz, aplicar Gauss y así ya tener una ecuación fácil de resolver y poder decifrar el valor de nuestras incógnitas.
El método de resolución es simple, de las ecuaciones dadas por ejemplo: 2x + 3y –z=3 como primera ecuación nuestra primer fila de la matriz seria [2 3 -1 | 3] es decir en orden los datos de nuestras incógnitas. Y separado por una barra vertical, solo para saber que es nuestro resultado pero que igual intervendrá al momento de hacer el Gauss, nuestro resultado.
Veamos un ejemplo de como ordenar ecuaciones a matrices. Tenemos 2 ecuaciones, 2x+5y=2 y x+7y=1. Para ponerlas en matriz seguimos nuestra condición anterior y tenemos que la matriz A, por llamarla de alguna manera, es:
[2 5 | 2]
[1 7 | 1]
Esa es la manera de como pasar nuestras ecuaciones a matrices y ya una vez hecha la matriz podemos pasar a aplicar Gauss para poder ya tener una ecuación sencilla y fácil de despejar que nos deje saber el valor de nuestras incógnitas.
Es muy importante tener en cuenta que se sigue un orden para poner los datos de la ecuación en la matriz y se debe de respetar a la hora de que querer resolverlas y sacar el resultado de la incógnita.
Veamos unos ejemplos para dejar claro todo el método de resolución.
- Tenemos las siguientes 3 ecuaciones
2x+3y-5z = -11
4x-7y+2z = 15
-2x +4y-6z = -18
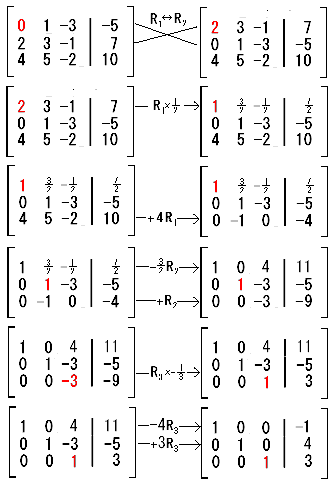
Para poder encontrar nuestras incógnitas es necesario aplicar Gauss empezando primero por las ecuaciones expresarlas en Matriz quedando todo de la siguiente manera :
[2 3 -5] [-11]
[4 -7 2] = [15]
[-2 4 -6] [-18]
Para empezar a aplicar el Gauss solo unimos con la separación de una linea puntada o una linea normal nuestra matriz principal con la de resultados, ya que aplicando Gauss a todo es la manera de encontrar los resultados. Nos queda:
[2 3 -5 | -11]
[4 -7 2 | 15]
[-2 4 -6 | -18]
Ahora si, ya con nuestra matriz bien hecha pasamos a resolver por Gauss. Empezamos:
Cambiar R1 por R3 R= Renglón
[-2 4 -6 | -18]
[4 -7 2 | 15]
[2 3 -5 | -11]
Dividir R1 entre -2
[1 -2 3 | 9]
[4 -7 2 |15]
[2 3 -5 |-11]
Multiplicar R1 por -4 y sumarle R2 y Multiplicar R1 por -2 y sumarle R3
[1 -2 3 | 9]
[0 1 -10 | -21]
[0 7 -11 | -29]
Multiplicar R2 por -7 y sumarle R3
[1 -2 3 | 9]
[0 1 -10 | -21]
[0 0 59 | 118]
Por ultimo dividimos R3 entre 59
[1 -2 3 | 9]
[0 1 -10 | -21]
[0 0 1 | 2]
Ahora para saber el valor de nuestras incógnitas empezamos desde R3 que ya esta muy obvio y es fácil de definir para resolver nuestras otras dos.
De R3 z=2
De R2 tenemos y – 10z= -21
Al ser z=2 sustituimos y nos queda:
DeR3 2y -20=-21
Y = -1
Y De R1 tenemos x -2y + 3z = 9
Sustituimos y y z nos queda:
X – 2(-1) + 3(2) = 9
X + 2 + 6 = 9
X = 1
Así es la manera de resolver un sistema de ecuaciones por Gauss, ahora veremos un segundo ejemplo para aclarar algunas dudas.
- Tenemos las ecuaciones
X – 2y + 3z = ½
4x + y – z = 13/6
2x – y + 3z = 3/2
Convertimos nuestras ecuaciones a Matriz, saltándonos ya un paso solo una matriz con la linea que divide los factores de las incógnitas con el resultado.
[1 -2 3 | ½]
[4 1 -1 | 13/6]
[2 -1 3 | 3/2]
Ahora empezamos a hacer el Gauss para tener nuestra Matriz con 1 en la diagonal y ceros debajo de ella.
Como ya tenemos nuestro primer uno empezamos a hacer ceros todos los de esa columna para eso multiplicamos por -4 R1 y le sumamos R2 y multiplicamos por -2 R1 y le sumamos R3, nos queda nuestra matriz:
[1 -2 3 | ½]
[0 9 -13 | 1/6]
[0 3 -3 | ½]
Para evitar manejar fracciones algo complejas tan temprano cambiamos R2 por el R3 y dividimos nuestro Nuevo R2 entre 3, tenemos:
[1 -2 3 | ½]
[0 1 -1 | 1/6]
[0 9 -13 | 1/6]
Ahora multiplicamos por -9 R2 y le sumamos R3
[1 -2 3 | ½]
[0 1 -1 | 1/6]
[0 0 -4 | -8/6]
Dividimos R3 entre 4 para encontrar nuestra primera incógnita por lo que nuestra matriz queda:
[1 -2 3 | ½]
[0 1 -1 | 1/6]
[0 0 1 | 1/3]
Por lo tanto
Z=1/3
Y= 1/6 + 1/3
Y= ½
X = 2(1/2) – 3(1/3) -1/2
X = ½
Y es de esta manera como se resuelve con Gauss un sistema de ecuaciones.
Unas notas que es importante tener en cuenta a la hora de resolver son las siguientes:
- Cuando el ultimo renglón da puros 0’s en la matriz quiere decir que tiene un numero infinito de soluciones.
- Cuando el ultimo renglón tiene 0’s en sus factores de incógnitas y un numero diferente a 0 en la parte de resultado de la matriz la que va después de este signo ‘|’ quiere decir que la incógnita que tocaba en ese renglón tiene un numero infinito de soluciones y solo necesitas resolver las otras en base a la incógnita sin solución definida. Por ejemplo: si el renglón donde sale z tiene todos 0’s y el de y es 0 1 1 | 2 entonces y = 2-z.
Aquí les dejamos unos ejercicios para resolver y seguir practicando el método de Gauss:
1. 3x + 6y – 6z = 9
2x – 5y + 4z = 6
5x + 28y -26z = -8
2. 9x + 9y -7z = 6
-7x + 0y –z = -10
9x + 6y + 8z = 45
3. x -2y + 3x = 11
4x + y -z = 4
2x –y + 3z = 10