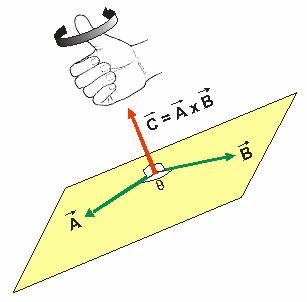
 El producto de vectores u y v es otro vector, su dirección es perpendicular a los dos vectores, su sentido está dado por la regla de la mano derecha, su magnitud es:
El producto de vectores u y v es otro vector, su dirección es perpendicular a los dos vectores, su sentido está dado por la regla de la mano derecha, su magnitud es:
\begin{align}\left| \overset{\rightarrow}{u} \right| \left| \overset{}{} \overset{\rightarrow}{v} \right| {sen } \alpha\end{align}
α es el ángulo entre los dos vectores.
Al producto de vectores también se le conoce como producto cruz para no confundir el signo × con una equis.
El producto de vectores se puede expresar con determinantes:
\begin{align}\overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
\left(\begin{array}{ccc}
\overset{\rightarrow}{i} & \overset{\rightarrow}{j} &
\overset{\rightarrow}{k}\\
u_{1} & u_{2} & u_{3}\\
v_{1} & v_{2} & v_{3}
\end{array}\right) = \left(\begin{array}{cc}
u_{2} & u_{3}\\
v_{2} & v_{3}
\end{array}\right) \overset{\rightarrow}{i} – \left(\begin{array}{cc}
u_{1} & u_{3}\\
v_{1} & v_{3}
\end{array}\right) \overset{\rightarrow}{j} + \left(\begin{array}{cc}
u_{1} & u_{2}\\
v_{1} & v_{2}
\end{array}\right) \overset{\rightarrow}{k}\end{align}
ó
\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}
Propiedades del producto de vectores
- Anticonmutativa \begin{align}\overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =-
\overset{\rightarrow}{v} \times \overset{\rightarrow}{u}\end{align} - Homogénea \begin{align}\beta \left( \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} \right)
= \beta \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
\overset{\rightarrow}{u} \times \overset{\rightarrow}{\beta v}\end{align} - Distributiva \begin{align}\overset{\rightarrow}{u} \times \left( \overset{\rightarrow}{v} +
\overset{\rightarrow}{w} \right) = \overset{\rightarrow}{u} \times
\overset{\rightarrow}{v} + \overset{\rightarrow}{u} \times
\overset{\rightarrow}{w}\end{align} - El producto de dos vectores paralelos es igual al vector nulo (cero) \begin{align}\overset{\rightarrow}{u} \| \overset{\rightarrow}{ v} ,
\overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
\overset{\rightarrow}{0}\end{align} - El producto de dos vectores es perpendicular a cada uno de los vectores.
Ejemplos
1. a = {3 i; -5 j; 2 k}
b = {4 i; -3 j; 5 k}
\begin{align}\overset{}{} \overset{\rightarrow}{a} \times \overset{\rightarrow}{b} = ( -5
( 5 ) – ( -3 ) 2 ) i- ( 3 ( 5 ) -4 ( 2 ) ) j+ ( 3 ( -3 ) -4 ( -5 ) ) k\end{align}
\begin{align}\overset{}{} \overset{\rightarrow}{a} \times \overset{\rightarrow}{b} = (
-25–6 ) i- ( 15-8 ) j+ ( -9–20 ) k\end{align}
\begin{align}\overset{}{} \overset{\rightarrow}{a} \times \overset{\rightarrow}{b} =
-19i-7j+11k\end{align}
2. a = {12 i; 6 j; -1 k}
b = {2 i; 7 j; -4 k}
\begin{align}\overset{}{} \overset{\rightarrow}{a} \times \overset{\rightarrow}{b} = ( 6
( -4 ) – ( -1 ) 7 ) i- ( 12 ( -4 ) – ( -1 ) 2 ) j+ ( 12 ( 7 ) -6 ( 2 ) ) k\end{align}
\begin{align}\overset{}{} \overset{\rightarrow}{a} \times \overset{\rightarrow}{b} = (
-24–7 ) i- ( -48–2 ) j+ ( 84-12 ) k\end{align}
\begin{align}\overset{}{} \overset{\rightarrow}{a} \times \overset{\rightarrow}{b} =
-17i+46j+72k\end{align}