Esto es para vectores en tercera dimension (3D).
Primero analizaremos las rectas y después el plano.
La recta en el espacio es una linea recta que cruz todo el plano tocando la punta o el fin de los 3 vectores colocados en el plano.
Se analiza de la siguiente forma:
Teniendo P=(X1,Y1,Z1), Q=(X2,Y2,Z2) y R(x,y,z).
A partir de estas tenemos que:
Vector PQ = V = (X2-X1)i + (Y2-Y1)j + (Z2-Z1)k
Vector PR = QR – QP
Vector QR = PR + QP
Entonces: PR=TPQ Donde T es una constante de proporción y sustituyendo PQ por V nos queda como ecuación PR=TV.
PR=TV es nuestra ecuación vectorial de una recta en el espacio pero ya desarrollada, es decir, nuestra ecuación general seria la siguiente:
Xi + Yj + Zk = X1i + Y1j + Z1k + TV ; Que es igual a:
Xi + Yj + Zk = X1i + Y1j + Z1k + T(X2-X1) i + T(Y2-Y1)j + T(Z2-Z1)k
Esta ecuación de arriba es ya la ECUACIÓN VECTORIAL DE UNA RECTA EN EL ESPACIO.
Ahora, para sacar valores de X,Y y Z tenemos las Ecuaciones Paramétricas que son las siguientes:
X = X1 + T(X2-X1)
Y= Y1 + T(Y2-Y1)
Z = Z1 + T(Z2-Z1)
Y también a raíz de estas tenemos las Ecuaciones Simétricas que son:
T = X-X1 / X2-X1 = Y-Y1 / Y2-Y1 = Z-Z1 / Z2-Z1
Vamos representando todo en ejemplos para aclarar todas las formulas.
1. Sea el punto P=(1, 3, 4) y Q=(2, 0, -4), Calcula la ecuación vectorial de la recta en el espacio, y sus ecuaciones paramétricas y simétricas.
Al darnos estos puntos rápido inferimos que nuestro punto R va a ser igual a (X,Y,Z).
Ahora pasamos a sustituir nuestros datos del ejercicio en la ecuación vectorial y tenemos:
Xi + Yj + Zk = i + 3j + 4k + Ti – 3Tj – 8Tk
Siguiente a esto sacamos nuestros valores de X, Y y Z que son nuestras ecuaciones paramétricas, entonces las ecuaciones nos quedan:
X = 1 + T
Y = 3 – 3T
Z = 4 – 8T
Y por último la ecuación simétrica:
X-1/1 = Y-3/-3 = Z-4/-8
Esta es la manera de resolver rectas en el espacio.
Ahora toca ver el plano en el espacio.
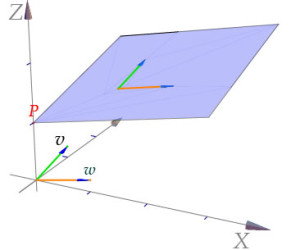
Plano en el Espacio
Lo que pasa aquí es que se genera un espacio en el plano, una especie de rectángulo y se calcula de la siguiente manera:
Teniendo n = ai + bj + ck, P=(Xo,Yo,Zo) y Q=(X,Y,Z), donde P es un punto cualquiera en el espacio, n es un vector dado que parte P y Q es un punto cualesquiera en un plano. Tenemos que:
PQ=(X-Xo)i + (Y-Yo)j + (Z-Zo)k, Si n es ortogonal a PQ entonces n.PQ =0 y eso es igual a:
a(X-Xo) + b(Y-Yo) + c(Z-Zo) = 0, desarrollado
aX-aXo+bY-bYo+cZ-cZo = 0;
aX + bY + cZ = aXo + bYo + cZo;
Y teniendo que aXo + bYo + cZo = 0 Entonces nuestra ECUACION DEL PLANO ES:
π = aX + bY + cZ = d
Donde d es la suma de la multiplicación de los valores de a,b y c por Xo,Yo y Zo respectivamente.
Un ejemplo practico para que quede claro:
2. Teniendo el punto P=(2,5,1) y la ecuación n=i-2j+3k calcular la Ecuación del Plano.
Con el punto P=(2,5,1) y ya la ecuación n = i-2j+3k se infiere rápido que Q como es un punto cualesquiera lo definimos como (X,Y,Z) entonces empezamos a definir variables de a,b,c y Xo, Yo y Zo, (a,b,c) sale de n y (Xo,Yo,Zo) sale de p entonces tenemos:
a=1, b=-2, c=3 y Xo=2, Yo=5, Zo=1
Sustituimos en la ecuación del plano y nos queda:
π=ax+by+cz = d;
π = x – 2y + 3z = 2(1) +(-2)(5) + 3(1)
π = x – 2y + 3z = -5
Y esa es la forma de sacar nuestra ecuación del plano.
A continuación mas ejercicios para repasar estos temas:
1. Teniendo el punto P=(3,5,2) y Q=(1,4,7). Calcula la ecuación vectorial de la recta en el espacio, y sus ecuaciones paramétricas y simétricas.
2. Teniendo el punto P=(1,3,6) y Q=(2,5,1). Calcula la ecuación vectorial de la recta en el espacio, y sus ecuaciones paramétricas y simétricas.
3. Teniendo P=(1,2,1) y n = -i+9j+6k. Calcula la ecuación del plano.