Ejemplos resueltos de multiplicación de vectores

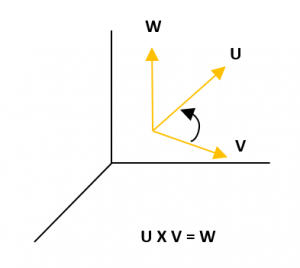
En estos ejercicios se tienen los vectores u = {u₁, u₂, u₃} y v = {v₁, v₂, v₃} y se sustituye en la formula para obtener W = U x V.

1.-  u = {3 i; -5 j; 2 k}

v = {-4 i; 1 j; 6 k}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = ( -5
(6) – 1(2) i- (3 (6 ) -(-4) ( 2 ) ) j+ (3 (1) -(-4) ( -5) ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
-30-2) i- (18+8) j+ ( 3-20 ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
-32i-26j-17k\end{align}

2.- u = {7 i; -5 j; 3 k}

v = {-6 i; 2 j; 4 k}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = ( (-5)
( 4) – (2) 3 ) i- (7 ( 4 ) -(-6) 3) j+ ( 7 ( 2) -(-6) (-5) ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
-20-6) i- (28+18) j+ ( 14-30) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
-26i-46j-16k\end{align}

3.- u = {5 i; 6 j; -3 k}

v = {5 i; 4 j; -7 k}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = ( 6
( -7 ) – 4 (-3) ) i- ( 5( -7 ) -5( -3 ) ) j+ ( 5( 4 ) -5 ( 6) ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
-42+12) i- ( -35+15) j+ ( 20-30 ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
-30i+20j-10k\end{align}

4.- u = {3 i; -1 j; -2 k}

v = {2 i; 4 j; 3 k}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = ( -1
( 3) – 4(-2) ) i- ( 3 (3 ) -2 ( -2 ) ) j+ ( 3 ( 4 ) -2 ( -1) ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
-3+8) i- ( 9+4) j+ ( 12+2 ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
5i-13j+14k\end{align}

5.- u = {6 i; 7 j; 8 k}

v = {-2 i; -2 j; -2 k}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = ( 7
( -2 ) – (-2) 8) i- ( 6 (-2 ) – 8( -2 ) ) j+ ( 6 ( -2 ) -(-2) 7 ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
-14+16) i- (-12+16) j+ ( -12+14 ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
2i-4j+2k\end{align}

6.- u = {-1 i; 5 j; 5 k}

v = {9 i; -3 j; 10 k}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = ( 5
( 10 ) – (-3) 5 ) i- ( -1 (10 ) -9 ( 5 ) ) j+ ( -1 ( -3 ) -9 ( 5) ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
50+15) i- ( -10-45) j+ ( 3-45 ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
65i+55j-42k\end{align}

7.- u = {-6 i; -1 j; -3 k}

v = {-1 i; -5 j; -4 k}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = ( -1
( -4 ) – (-5) (-3) ) i- (-6 ( -4 ) -(-1) ( -3 ) ) j+ ( -6 ( -5 ) -(-1) ( -1) ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
4-15) i- (24-3) j+ ( 30-1 ) k\end{align}

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
-11i-21j+29k\end{align}