Te invito a realizar este ejercicio test sobre conjuntos. ¿Cuánto sabes sobre el tema? Lo descubrirás de inmediato, porque este desafío de diez preguntas te devuelve el resultado al finalizarlo.
Estamos hablando de ejercicios básicos sobre conjunto, que incluyen temas como unión e intersección de conjuntos, pertenencia e inclusión en conjuntos entre otras cuestiones. Hay ejercicios planteados con letras y con gráficos (diagramas de Venn) para que realices propuestas variadas y divertidas a la vez.
Te propongo entonces, realizar este ejercicio test para evaluar cuánto sabes o cuánto recuerdas acerca de este tema. Toma el tiempo que quieras e incluso es buena idea que tengas a mano lápiz y papel. Si una vez que lo realices, los resultados obtenidos no te satisfacen, más abajo en este mismo post repasamos los principales conceptos sobre conjuntos, de tal modo que puedas releerlos y razonarlos teniendo la oportunidad de volver a realizar el ejercicio test sobre conjuntos, tantas veces como desees.
Ejercicio test sobre conjuntos
Repaso de temas sobre conjuntos
- Relación de pertenencia
La relación de pertenencia sólo se da entre los elementos de un conjunto y éste. Es decir es perfectamente correcto decir que uno o más elementos pertenecen a un conjunto. En este caso, nunca debe usarse la palabra inclusión, por tanto no es correcto decir que un elemento está incluido en un conjunto.
- Relación de inclusión
La relación de inclusión, se da entre conjuntos y sub conjuntos. Es correcto decir que un subconjunto está incluido en un conjunto mayor, pero no es correcto decir que un subconjunto pertenece a un conjunto mayor.
- Concepto de subconjunto
Decimos que el conjunto A es un subconjunto del conjunto B, sí y sólo sí, todo elemento del conjunto A es también elemento del conjunto B.
Cuando trabajamos antes la relación de inclusión, decíamos que es correcto expresar esta relación (que A es un subconjunto de B) diciendo también que “A está incluido en B”. Utilizando el lenguaje o símbolos matemáticos, esto se expresa de la siguente manera
A ⊂ B
Es posible realizar esta misma afirmación, pero diciendo que el conjunto B contiene al conjunto A, o -lo que es lo mismo- que el conjunto B incluye al conjunto A. Esto también puede escribirse con símbolos matemáticos:
B ⊃ A
¿Te gustaría que pusiera un ejemplo real? Mira es muy sencillo: llamemos B al conjunto de los habitantes de la ciudad de Bogotá y C al conjunto de los habitantes de Colombia. Es claro y correcto decir, que los habitantes de Bogotá son un subconjunto de los habitantes de Colombia. Esto se expresaría en símbolos, de la siguiente manera:
B ⊂ C
lo que significa que B está incluido en C.
- ¿Qué significa unir dos o más conjuntos?
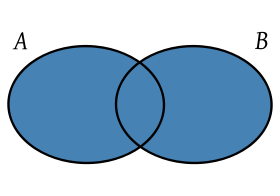
La operación se denomina unión de conjuntos, y da como resultado un nuevo conjunto formado por todos los elementos que pertenecen a ambos conjuntos. Escrito con símbolos, la unión de dos conjuntos (por ejemplo llamados G y H) se denota así:
G ∪ H
- ¿Qué es intersección de conjuntos?
Realizar la intersección de dos o más conjuntos, es definir un nuevo conjunto formado solamente por aquellos elementos que estén presentes en todos los conjuntos en cuestión. En otras palabras: sólo forman parte del nuevo conjunto, los elementos que tengan en común.
Existe un símbolo matemático para la intersección. Para poner un ejemplo, la intersección de dos conjuntos llamados G y H se denota de la siguiente manera:
G ∩ H
Imagen: es.wikipedia
