 Antes de mostrar como resolver las integrales de funciones trigonométricas hay que definir que es una integral.
Antes de mostrar como resolver las integrales de funciones trigonométricas hay que definir que es una integral.
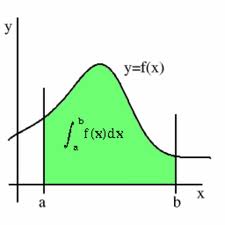
Una integral se define gráficamente como el área bajo la curva entre dos valores determinados de x. En algunos textos a la integración se le llama antiderivación.
Integrales de funciones trigonométricas
Para resolver integrales de funciones trigonométricas existen las siguientes fórmulas:
\begin{align} 1. \int {sen} u {du} =- \cos u +c \end{align}
\begin{align} 2. \int \cos u {du} = {sen} u +c \end{align}
\begin{align} 3. \int \tan u {du} = \ln | \sec u | +c \end{align}
\begin{align} 4. \int \cot u {du} = \ln | {sen} u | +c \end{align}
\begin{align} 5. \int \sec u {du} = \ln | \sec u + \tan u | +c \end{align}
\begin{align} 6. \int \csc u {du} = \ln | \csc u – {cotu} | +c \end{align}
\begin{align} 7 \int \sec^{2} u ^{} {du} = \tan u +c \end{align}
\begin{align}8. \int \csc^{2} u ^{} {du} =- \cot u +c\end{align}
\begin{align}9. \int \sec u \tan u {du} = \sec u +c \end{align}
\begin{align} 10. \int \csc u \cot u {du} = – \csc u +c\end{align}
Existen dos casos en las integrales:
1. Cuando la “x” está sola, se aplican las fórmulas fundamentales de integración de manera directa.
Ejemplo de integrales de funciones trigonométricas cuando la x está sola:
\begin{align} \int {sen} 2x {dx} =- \cos 2x +c\end{align}
La diferencial de una función es la derivada de esta multiplicada por “dx”.
2. Cuando la “x” está acompañada, lo primero que se hace es “sacar la diferencial de lo que está dentro del paréntesis. Si la diferencial ya está completa se aplican directamente las fórmulas fundamentales de integración” en caso de que no este completa la diferencial, primero se debe completar y después aplicar las fórmulas fundamentales de integración.
Ejemplo de integrales de funciones trigonométricas cuando la x está acompañada:
\begin{align} \int \frac{{sen} 2x}{\sqrt{36-9 {sen}^{2} x}} {dx} \end{align}
\begin{align}- \frac{1}{18} 2 \int \frac{{sen} x \cos x}{\sqrt{36-9{sen}^{2} x}} {dx} \end{align}
\begin{align}- \frac{2}{9} \sqrt{36-9 {sen}^{2} x} +c \end{align}
También nos podemos apoyar en las identidades trigonométricas para resolver las integrales.
Identidades trigonométricas
Recíprocos
\begin{align} {sen} ( A ) = \frac{1}{\csc ( A )} \csc ( A ) =
\frac{1}{{sen} ( A )} \cos ( A ) = \frac{1}{\sec ( A )} \sec ( A ) = \frac{1}{\cos ( A )} \tan ( A ) = \frac{1}{\cot ( A )} \cot ( A ) = \frac{1}{\tan ( A )}\end{align}
Pitagóricas
\begin{align} {sen}^{2} ( A ) + \cos^{2} ( A ) = 1 \end{align}
\begin{align} 1+ \tan^{2} ( A ) = \sec^{2} ( A ) \end{align}
\begin{align} 1+ \cot^{2} ( A ) = \csc^{2} ( A ) \end{align}
Ángulos negativos
\begin{align}{sen} ( -A ) =- {sen} ( A ) \end{align}
\begin{align}\cos ( -A ) = \cos ( A ) \end{align}
\begin{align}\tan ( -A ) =- \tan ( A )\end{align}
Suma de Ángulos
\begin{align}{sen} ( A+B ) = {senAcosB} + {cosAsenB} \end{align}
\begin{align} \cos ( A+B ) = {cosAcosB} – {senAsenB} \end{align}
\begin{align} \tan ( A+B ) = \frac{\tan ( A ) + \tan ( B )}{1- \tan ( A ) \tan ( B )} \end{align}
Diferencia de Ángulos
\begin{align}{sen} ( A-B ) = {senAcosB} – {cosAsenB} \end{align}
\begin{align} \cos ( A-B ) = {cosAcosB} + {senAsenB} \end{align}
\begin{align} \tan ( A-B ) = \frac{\tan ( A ) – \tan ( B )}{1+ \tan ( A ) \tan ( B )} \end{align}
Ángulos dobles
\begin{align}{sen} ( 2A ) =2 {sen} ( A ) \cos ( A ) \end{align}
\begin{align}\cos ( 2A ) = \cos^{2} ( A ) – {sen}^{2} ( A ) =1-2 {sen}^{2} ( A) =2 \cos^{2} ( A ) -1 \end{align}
\begin{align} \tan ( 2A ) = \frac{2 \tan ( A )}{1-tan^{2} ( A )} \end{align}
Productos
\begin{align} 2 {sen} ( A ) \cos ( B ) = {sen} ( A+B ) + {sen} ( A-B ) \end{align}
\begin{align}2 \cos ( A ) {sen} ( B ) = {sen} ( A+B ) – {sen} ( A-B ) \end{align}
\begin{align}2 \cos ( A ) \cos ( B ) = \cos ( A+B ) + \cos ( A-B ) \end{align}
\begin{align} 2 {sen} ( A ) {sen} ( B ) = \cos ( A+B ) – \cos ( A-B ) \end{align}
Despejes importantes
\begin{align}{sen}^{2} ( A ) = \frac{1}{2} [ 1- \cos ( 2A ) ] \end{align}
\begin{align}\cos^{2} ( A ) = \frac{1}{2} [ 1+ \cos ( 2A ) ] \end{align}
\begin{align}{sen}^{2} ( A ) =1- \cos^{2} ( A ) \end{align}
\begin{align}\cos^{2} ( A ) =1- {sen}^{2} ( A ) \end{align}
\begin{align} \tan^{2} ( A ) = \sec^{2} ( A ) -1 \end{align}
\begin{align} \cot^{2} ( A ) = \csc^{2} ( A ) -1 \end{align}
Con ayuda de las fórmulas de integración y las identidades trigonométricas ya puedes resolver una integral de una función trigonométrica!