Parábola con vértice en un punto cualquiera

Una parábola  es la sección cónica que resulta de cortar un cono con un plano cuyo ángulo de inclinación respecto al eje del cono es igual al presentado por su directriz, es decir el plano es paralelo a la recta. En este artículo veremos como encontrar la ecuación de la parábola con vértice en un punto cualquiera.

Parábola

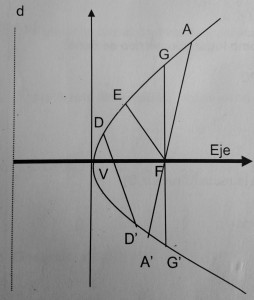
Los elementos de la parábola son los siguientes:

1. El punto fijo se llama foco (F).
2. La recta fija se llama directriz, (d).
3. La recta que pasa por el foco y es perpendicular a la directriz se le llama eje de simetría de la parábola.
4. El punto medio del foco a la recta fija directriz se llama vértice (V).
5. El segmento que uno el foto con cualquier punto de la parábola se llama radio vector (EF) .
6. La recta que uno dos puntos de la parábola se llama cuerda (DD’).
7. La cuerda que pasa por el foco se llama cuerda focal (AA’).
8. La cuerda focal perpendicular al eje se simetría se llama lado recto (GG’).
9. La distancia del pertice al foco se llama parámetro p.

Con estos elementos podemos definir a la parábola como: el lugar geométrico de un punto que se mueve en un plano de tal manera que su distancia a una recta fija, situada en el plano, es siempre igual a su distancia a un punto fijo del plano y que no pertenece a la recta.

Formulario para parábola con vértice en un punto cualquiera

NOTA: este formulario se usa cuando vas a calcular “p” con distancia dirigida, es decir positiva (si está abierta hacia la derecha o hacia arriba) o “p” negativa (cuando está abierta a la izquierda o hacia abajo).

NOTA: este formulario se usa cuando vas a calcular “p” valor absoluto es decir siempre positivo.