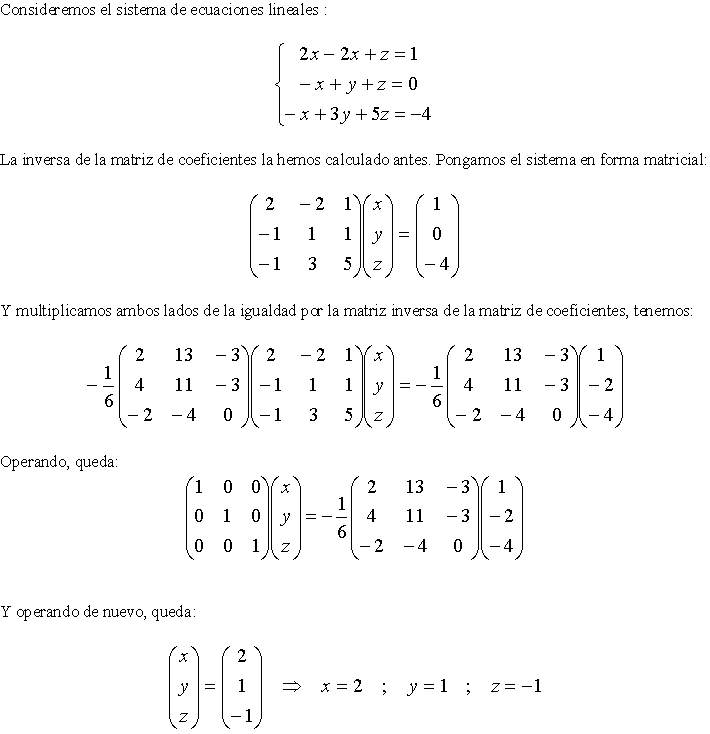Para calcular la Matriz Inversa es de la siguiente manera:
A^-1 = 1/DA x (Matriz adjunta de A)
Determinante de la Matriz A tiene que ser Diferente de 0.
Matriz Adjunta de A: Transpuesta de la matriz de cofactores de A.
Transpuesta: Cambiar las filas por columnas de la matriz.
Matriz de cofactores
- Obtener los menores de cada termino
- Multiplicarlo por el signo que le corresponde
- Obtener el cofactor de cada menor(Determinante)
- Armar la matriz de cofactores
En pocas palabras es encontrar la matriz inversa por medio de determinantes y a continuación se vera como.
Aquí un ejemplo para que quede mas claro en que consiste la Matriz Inversa por cofactores:
- [2 4 3]
[0 1 -1]
[3 5 7]
Lo primero que hay que hacer es sacar el determinante a la matriz que tenemos
[2 4 3] 2 4
[0 1 -1] 0 1
[3 5 7] 3 5
Det = (14-12+0) – (9-10+0) = 2 + 1
Det = 3
Ahora empieza prácticamente el método, según nuestra matriz de signos y aplicamos el método de cofactores visto previamente en determinantes por lo que agarramos la primera fila y a partir de ahi empezamos a aplicar por lo que tenemos:
a11 +[1 -1] a12 –[0 -1] a13+[0 1]
[5 7] [3 7] [3 5]
a21 –[4 3] a22 +[2 3] a23 –[2 4]
[5 7] [3 7] [3 5]
a31 +[4 3] a32 –[2 3] a33 +[2 4]
[1 -1] [3 7] [3 5]
Sacamos nuestra matriz calculando los determinantes de cada espacio y tenemos:
a11 Det=12 a12 Det=-3 a13 Det=-3
a21 Det=-13 a22 Det=5 a23 Det=2
a31 Det=-7 a32 Det=2 a33 Det=2
Los colocamos en una matriz y nos queda:
[12 -3 -3]
[-13 5 2]
[-7 2 2]
Ahora para sacar la matriz adjunta tenemos que cambiar las filas por las columna de modo que nuestra matriz adjunta nos queda:
[12 -13 -7]
[-3 5 2]
[-3 2 2]
Y como tenemos arriba en las formulas, nuestra matriz inversa sera la multiplicación de 1/DA por la matriz adjunta y sera:
A^-1 = 1/3 [12 -13 -7]
[-3 5 2]
[-3 2 2]
La manera para comprobar si estamos o no en lo correcto es multiplicar la matriz adjunta por la original y nos tiene que dar como resultado la matriz identidad.
Otro ejemplo para aclarar dudas de como realizar este método
2. [9 3 9]
[6 -10 4]
[10 7 5]
Sacamos el determinante de la matriz
[9 3 9] 9 3
[6 -10 4] 6 -10
[10 7 5] 10 7
Det = (-450+120+378) – (-900+252+90) = 606
Det = 606
Continuamos con sacar el determinante de la matriz por el metodo de cofactores escogiendo la primera fila y tenemos:
a11 +[-10 4] a12 –[6 4] a13+[6 -10]
[7 5] [10 5] [10 7]
a21 –[3 9] a22 +[9 9] a23 –[9 3]
[7 5] [10 5] [10 5]
a31 +[3 9] a32 –[9 9] a33 +[9 3]
[-10 4] [6 4] [6 -10]
Sacamos nuestra matriz calculando los determinantes de cada espacio y tenemos:
a11 Det=-78 a12 Det=10 a13 Det=142
a21 Det=48 a22 Det=-45 a23 Det=-33
a31 Det=102 a32 Det=18 a33 Det=-108
Los colocamos en una matriz y nos queda:
[-78 10 142]
[48 -45-33]
[102 18 -108]
Para sacar nuestra matriz adjunta cambiamos las filas por las columnas y nos queda:
[-78 48 102]
[10 -45 18]
[142 -33 -108]
Y como tenemos arriba en las formulas, nuestra matriz inversa sera la multiplicación de 1/DA por la matriz adjunta y sera:
A^-1 = 1/606 [-78 48 102]
[10 -45 18]
[142 -33 -108]
Y así es como sacamos la matriz inversa por medio de cofactores.
Mas ejercicios de matriz inversa por medio de cofactores:
1.
[2 5 -1]
[4 1 3]
[-2 2 0]
2.
[1 1 1]
[2 0 -1]
[1 3 6]