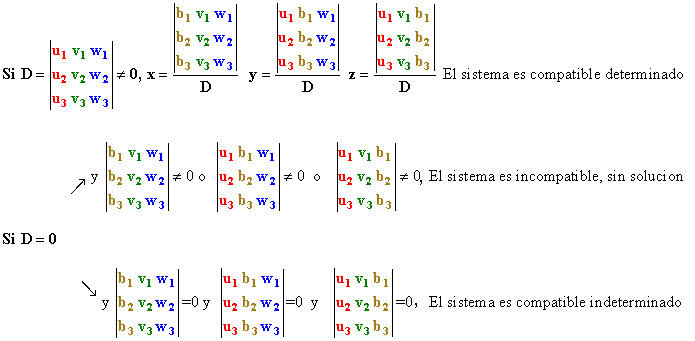Este método consiste en la resolución de sistema de ecuaciones por medio de determinantes.
Teniendo las ecuaciones de modo
a11X1 + a12X2 + … + a1nXn = b1
a21X1 + a22X2 + … + a2nXn = b2
… … …
an1X1 + an2X2 + … + annXn = bn
Lo pasamos a matriz y tenemos
[a11 a12 … a1n] [X1] [b1]
[a21 a22 … a2n] [X2] = [b2]
… … … … … …
[an1 an2 … ann] [Xn] [bn]
Para encontrar los valores de las incógnitas se hace de la siguiente manera:
Se sacara el determinante de la matriz original y después se sacara el determinante de la matriz con base a la incógnita sustituyendo los resultados de las ecuaciones según la incógnita de base de la matriz, aquí graficamente:
A=[a11 a21 … a1n]
[a21 a22 … a2n]
…
[an1 an2 … ann]
Det A
AX1=[b1 a21 … a1n]
[b2 a22 … a2n]
…
[bn an2 … ann]
Det AX1
AX2=[a11 b1 … a1n]
[a21 b2 … a2n]
…
[an1 bn … ann]
Det AX2
AXn=[a11 a12 … b1]
[a21 a22 … b2]
…
[an1 an2 … bn]
Det AXn
Ya con las determinantes de cada matriz se sustituyen los valores en las siguientes fórmulas:
X1 = DAX1 / DA
X2 = DAX2 / DA
Xn = DAXn / DA
Aqui un pequeño ejemplo:
3x+2y = 7
-x + 4y = 7
Primero hacemos matriz el sistema
A=[3 2]
[-1 4]
Ahora sacamos la determinante de la matriz A
Det A = 3×4 + -1(-2) = 12 + 2 = 14
Empezamos a hacer las matrices de las incógnitas y sacamos los determinantes de éstas
AX=[7 2]
[7 4]
Det AX = 7×4 + -(7×2) = 28 – 14 = 14
AY=[3 7]
[-1 7]
Det AY = 3×7 + -(-1×7) = 21 + 7 = 28
Ahora sustituimos en las formulas para sacar las incógnitas:
X=14/14=1
Y=28/14=2
Otro ejemplo con una matriz mas grande para dejar en claro el CRAMER:
2. 2X + 2y + Z = 7
X + 2Y + Z = 0
-X + Y + 3Z = 1
Convertimos el sistema de ecuaciones a matriz y sacamos su determinante
A= [2 2 1] 2 2
[1 2 1] 1 2
[-1 1 3] -1 3
Det A = (12+1-2) – (-2+6+2) = 5
Ahora hacemos las matrices según la incógnita y sacamos sus determinantes respectivos
AX = [7 2 1] 7 1
[0 2 1] 0 2
[1 1 3] 1 1
Det AX = (42+2+0) – (2 + 0 + 7) = 35
AY = [2 7 1] 2 7
[1 0 1] 1 0
[-1 1 3] -1 1
Det AY = (0-7+1) – (0+2+21) = -18
AZ = [2 2 7] 2 2
[1 2 0] 1 2
[-1 1 1] -1 2
Det AZ = (4+0+14) – (-14+0+2) = 30
Ahora calculamos nuestras incógnitas sustituyendo en las formulas y tenemos que:
X=35/5=7
Y=-18/5
Z=30/5 =6
Así es como se resuelve un sistema de ecuaciones por medio de este método que es el CRAMER.
Mas ejercicios a resolver con CRAMER:
1.
X1 + X2 + X3 = 6
2X1 + 0X2 – X3 = 4
X1 + 0X2 + 3X3 = 3
2.
2X + 5Y – Z = -1
4X + 2Y + 3Z = 6
-2X + 2Y + Z = 5