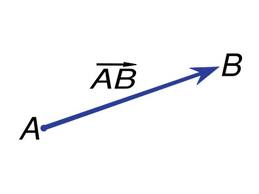
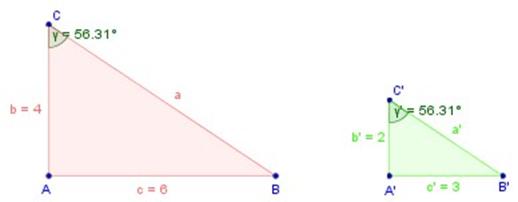
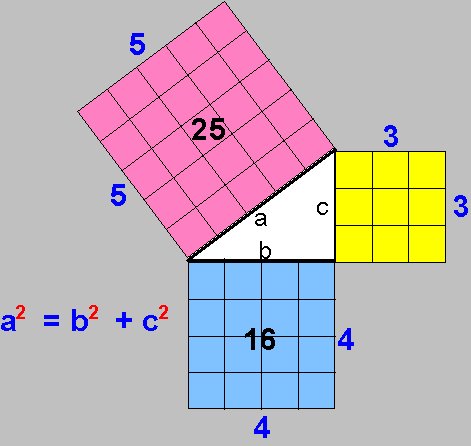
Los vectores son segmentos que se encuentran orientados, en donde uno de sus extremos es el origen y el otro es el objetivo, por lo que cuenta con magnitud, direccionalidad y sentido dentro del plano cartesiano. El estudio del espacio vectorial parte de sistemas de ecuaciones lineales y la geometría analítica, estos estudios tuvieron un mayor desarrollo en el siglo XVII en Europa, especialmente por matemáticos como Descartes, Fermat de Francia, y posteriormente por August Ferdinand, Giusto Bellavitis, Giusepe Peano, entre otros.
Vector AB
Suma de dos vectores:
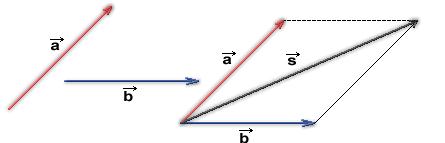
La suma geométrica de dos vectores es una ley que asocia un tercer vector a dos vectores dados por medio de la composición geométrica de la ley del paralelogramo, cuya ecuación es S= A+B, sin embargo, existen varias maneras de resolver una suma de vectores además de ésta, entre ellas podemos considerar al método del polígono, el método del triángulo, el método analítico, el método gráfico. Entre todas estas posibilidades la manera más sencilla de realizar una suma de dos vectores es utilizando el método del paralelogramo, porque así se puede ubicar la suma directamente sobre el plano cartesiano, y se puede ejecutar duplicando la medida de cada vector a sumar contrario a sí mismo dentro de la medida del otro, de tal manera que formará un paralelogramo y dará la medida exacta del tercer vector, hallando así el resultado de la suma, de allí viene el nombre del método.
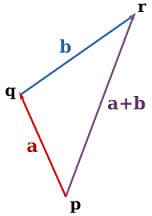
En el caso del método del triángulo, los vectores se trasladan sin ser modificados en sus propiedades conectándolos uno por el origen y otro por el objetivo, se podría decir entonces que lo que sería la “cabeza” de uno se conecta con lo que sería la “cola” del otro, sin importar el orden por ser una suma conmutativa, así pues, el vector que representa el resultado es el que se forma uniendo los extremos que quedan libres, se completa el triángulo uniendo las “cabezas” de los vectores que quedan en el extremo. En el siguiente ejemplo encontramos un vector a + b que corresponde al resultado de la suma, este es el vector resultante y se denomina vector s:
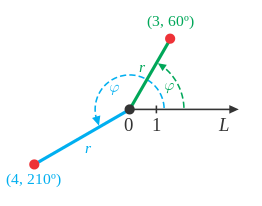
El método del paralelogramo puede ser utilizado como una alternativa al método del triángulo. Si por ejemplo el vector a y b tienen magnitudes iguales a 6.0 y 7.0, y forman un ángulo de 30°; calcular dirección y magnitud del vector s. Para realizar este cálculo podemos aplicar la Ley de Cosenos, teniendo en cuenta que los ángulos 
son suplementarios:
Para calcular la dirección del vector resultante es necesario hallar el valor del ángulo 
, para esto podemos utilizar la ley de senos como se muestra a continuación:
