Se llama elipse al lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos F y F’ es una cantidad constante, que se representa por 2a. Así, para cualquier punto M de la curva, se tiene MF + MF’ = 2a. En este artículo veremos como encontrar la ecuación de la elipse con centro en un punto cualquiera.
Se llama elipse al lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos F y F’ es una cantidad constante, que se representa por 2a. Así, para cualquier punto M de la curva, se tiene MF + MF’ = 2a. En este artículo veremos como encontrar la ecuación de la elipse con centro en un punto cualquiera.
Formulario para la elipse con centro en un punto cualquiera (h, k)
|
Fórmula de: |
Eje mayor paralelo a “x” |
Eje mayor paralelo a “y” |
|
Ecuación de la elipse |
\begin{align} \frac{(x-h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} =1 \end{align} |
\begin{align}\frac{(x-h)^{2}}{b^{2}} + \frac{(y-k)^{2}}{a^{2}} =1 \end{align} |
|
Focos |
F(h + c, k) F’(h – c, k) |
F(h, k + c) F’(h, k – c) |
|
Vértices del eje mayor |
V(h + a, k) V’(h – a, k) |
V(h, k + a) V’(h, k – a) |
|
Vértices del eje menor |
B(h, k + b) B’(h, k – b) |
B(h + b, k) B’(h – b, k) |
|
Longitud del eje mayor |
VV’=2a |
VV’=2a |
|
Longitud del eje menor |
BB’=2b |
BB’=2b |
|
Distancia focal |
FF’=2c |
FF’=2c |
|
Excentricidad |
e=c/a |
e=c/a |
|
Longitud del lado recto |
\begin{align} LR= \frac{2b^{2}}{a} \end{align} |
\begin{align} LR= \frac{2b^{2}}{a} \end{align} |
|
Relación pitagórica |
\begin{align} a^{2} =b^{2} +c^{2} \end{align} |
\begin{align} a^{2} =b^{2} +c^{2} \end{align} |
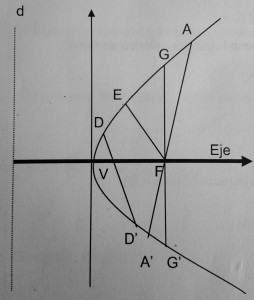
Elementos de la elipse
- Los puntos fijos F y F’ se llaman focos y la longitud FF’ distancia focal que se designa por 2c.
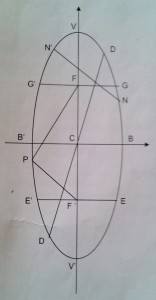
- El punto medio de FF’ es el centro de la elipse y se representa por C.
- Los segmentos PF y PF’ que une un punto cualquiera de la elipse con los focos se llaman radios.
- Un segmento que une dos puntos MN’ cualesquiera de la elipse se denomina cuerda.
- Una cuerda que pasa por el centro, tal como DD’, es un diámetro.
- El diámetro que pasa por los focos se llama eje mayor, o focal VV’, que se designa por 2a y el perpendicular a él es el eje menor o normal BB’, que se designa por 2b.
- Las intersecciones V, V’ y B, B’ de la elipse con los ejes son los vértices de las elipse.
- Las cuerdas EE’ y GG’ que pasan por los focos y son perpendiculares al eje mayor son los lados rectos de la elipse.
- Excentricidad de una elipse es la razón de la semidistancia focal al semieje mayor (c/a) y se prepresenta por e. paara que sea elipse c < a.
Propiedades de la elipse
- El eje mayor es igual a la cantidad constante VV’ = 2a
- El eje menor es igual BB’ = 2b
- La distancia focal FF’ = 2c
- Los ejes se cortan en su punto medio C
- El cuadrado del semieje mayor es igual a la suma de los cuadrados del semieje menor y de la semidistancia focal. \begin{align} a^{2} =b^{2} +c^{2} \end{align}
- La excentricidad es siempre menor que 1.