 En este artículo veremos el tema de derivadas algebraicas de funciones explícitas, primero tenemos que definir que es una derivada y que es una función explícita.
En este artículo veremos el tema de derivadas algebraicas de funciones explícitas, primero tenemos que definir que es una derivada y que es una función explícita.
Una función explícita es aquella donde la “y” está despejada. Gráficamente la derivada de una función es la pendiente de la recta tangente a una curva en un punto determinado de dicha curva.
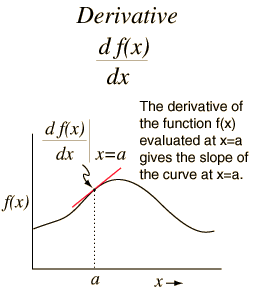
La nomenclatura para indicar la derivada de una función puede ser de tres formas
\begin{align}y’\end{align}
\begin{align}\frac{d y}{d x}\end{align}
\begin{align}f’ ( x )\end{align}
Todas las derivadas que veremos en este artículo serán con respecto de x.
Existen dos métodos para obtener la derivada de una función
1. Por definición: también llamada regla de los cuatro pasos, en donde se deberá aplicar el siguiente concepto:
\begin{align}\lim_{▵ x \longrightarrow 0} \frac{f ( x+▵ x ) -f ( x)}{▵ x}\end{align}
2. Por formula o teoremas.
Formulas de derivadas algebraicas de funciones explícitas
Estas fórmulas nos servirán para aplicarlas en las derivadas algebraicas de funciones explícitas.
\begin{align}1. \frac{d}{ {du}} ( {cu} ) = {cu}’ \end{align}
\begin{align} 2. \frac{d}{ {du}} ( u \pm v ) =u’ \pm v’ \end{align}
\begin{align} 3. \frac{d}{ {du}} ( u \cdot v ) = {uv}’ + {vu}’ \end{align}
\begin{align} 4. \frac{d}{ {du}} \left( \frac{u}{v} \right) = \frac{ {vu}’ –
{uv}’}{v^{2}} \end{align}
\begin{align} 5. \frac{d}{ {du}} ( c ) =0 , {la} c {es}
{una} {constante} \end{align}
\begin{align}6. \frac{d}{ {du}} ( u^{n} ) = {nu}^{n-1} u’ \end{align}
\begin{align}7. \frac{d}{ {du}} ( u ) =1 \end{align}
\begin{align}8. \frac{d}{ {du}} ( | u | ) = \frac{u}{| u |} u’ ,u \neq 0\end{align}
\begin{align} 9. \frac{d}{ {du}} ( \ln u ) = \frac{1}{u} \cdot u’ \end{align}
\begin{align}10. \frac{d}{ {du}} ( \log_{a} u ) = \frac{1}{u} \cdot \log_{a} e
\cdot u’ \end{align}
\begin{align} 11. \frac{d}{ {du}} ( e^{u} ) =e^{u} \cdot u’ \end{align}
\begin{align} 12. \frac{d}{ {du}} ( a^{u} ) =a^{u} \cdot \ln a \cdot u’ \end{align}
\begin{align} 13. \frac{d}{ {du}} ( {sen} u ) = \cos u \cdot u’ \end{align}
\begin{align} 14. \frac{d}{ {du}} ( \cos u ) =- {sen} u \cdot u’ \end{align}
\begin{align} 15. \frac{d}{ {du}} ( \tan u ) = \sec^{2} u \cdot u’ \end{align}
\begin{align} 16. \frac{d}{ {du}} ( \cot u ) = -\csc^{2} u \cdot u’ \end{align}
\begin{align} 17. \frac{d}{ {du}} ( \sec u ) = \sec u \cdot \tan u \cdot u’\end{align}
\begin{align}18. \frac{d}{ {du}} ( \csc u ) =- \csc u \cdot \cot u \cdot u’ \end{align}
\begin{align}19. \frac{d}{ {du}} ( {arcsen} u ) = \frac{1}{\sqrt{1-u^{2}}} u’
\end{align}
\begin{align} 20. \frac{d}{ {du}} ( \arccos u ) =- \frac{1}{\sqrt{1-u^{2}}} u’ \end{align}
\begin{align} 21. \frac{d}{ {du}} ( \arctan u ) = \frac{1}{\sqrt{1+u^{2}}} u’ \end{align}
\begin{align} 22. \frac{d}{ {du}} ( {arccot} u ) =- \frac{1}{\sqrt{1+u^{2}}} u’
\end{align}
\begin{align} 23. \frac{d}{ {du}} ( {arcsec} u ) = \frac{1}{u \sqrt{u^{2} -1}}u’ \end{align}
\begin{align} 24. \frac{d}{{du}} ( {arccsc} u ) =- \frac{1}{u \sqrt{u^{2} -1}}u’ \end{align}
\begin{align} 25. \frac{d}{{du}} ( {senhu} ) = {coshu} \cdot u’ \end{align}
\begin{align}26. \frac{d}{{du}} ( {coshu} ) = {senhu} \cdot u’ \end{align}
\begin{align}27. \frac{d}{{du}} ( {tanhu} ) = {sech}^{2} h \cdot u’ \end{align}
\begin{align}28. \frac{d}{{du}} ( {cothu} ) =- {csch}^{2} h \cdot u’\end{align}
\begin{align}29. \frac{d}{{du}} ( {sechu} ) =- {sechu} \cdot
{tanhu} \cdot u’ \end{align}
\begin{align} 30. \frac{d}{{du}} ( {cschu} ) =- {cschu} \cdot {cothu} \cdot u’ \end{align}





No hay respuetas