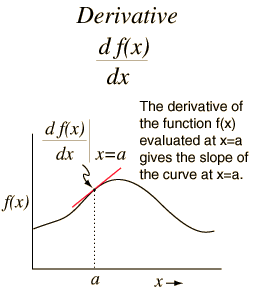
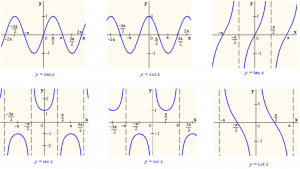
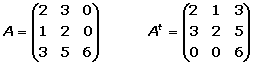 Ahora que ya sabes como se obtienen, te propongo los siguientes ejercicios de derivadas de las funciones trigonométricas para que practiques. Te pondré siete ejercicios para que intentes resolverlos con las formulas e identidades que puedes consultar en el artículo “Derivada de funciones trigonométricas“, y al final te pondré los resultados para que compruebes tus respuestas.
Ahora que ya sabes como se obtienen, te propongo los siguientes ejercicios de derivadas de las funciones trigonométricas para que practiques. Te pondré siete ejercicios para que intentes resolverlos con las formulas e identidades que puedes consultar en el artículo “Derivada de funciones trigonométricas“, y al final te pondré los resultados para que compruebes tus respuestas.
Además también puedes consultar todas las formulas de derivación.
Ejercicios
\begin{align}1. y= \tan ( x^{2} ) \end{align}
\begin{align} 2. y= \tan^{2} ( x^{} ) \end{align}
\begin{align} 3. y= \sec^{3} \sqrt{x} \end{align}
\begin{align} 4. y= \frac{1}{2} \tan ( x ) {sen} ( 2x ) \end{align}
\begin{align}5. y= – \frac{1}{4} \cos ( 4x ) + \frac{1}{12} \cos^{3} ( 4x ) \end{align}
\begin{align} 6. y= x^{2} {sen} ( x ) +2x \cos ( x ) -2 {sen} ( x ) \end{align}
\begin{align} 7 . y= \frac{1- {sen} ( x )}{1+ {sen} ( x )} \end{align}
Soluciones a derivadas de las funciones trigonométricas
\begin{align}1. y= \tan ( x^{2} ) \end{align}
\begin{align} y’ = \sec^{2} ( x^{2} ) \cdot 2x \end{align}
\begin{align} y’ =2 {xsec}^{2} ( x^{2} ) \end{align}
\begin{align} 2. y= \tan^{2} ( x^{} ) \end{align}
\begin{align} y= ( \tan ( x ) )^{2} \end{align}
\begin{align}y’ =2 \tan ( x ) \cdot \sec^{2} ( x ) \end{align}
\begin{align} 3. y= \sec^{3} \sqrt{x} \end{align}
\begin{align} y= \left( \sec \sqrt{x} \right)^{3}\end{align}
\begin{align} y’ =3 \left( \sec \sqrt{x} \right)^{2} \cdot \sec \sqrt{x} \cdot \tan
\sqrt{x} \cdot \frac{1}{2} x^{- \frac{1}{2}} \end{align}
\begin{align} y’ = \frac{3 \sec^{2} \sqrt{x} \cdot \sec \sqrt{x} \cdot \tan \sqrt{x}}{2
\sqrt{x}} \end{align}
\begin{align} 4. y= \frac{1}{2} \tan ( x ) {sen} ( 2x ) \end{align}
\begin{align} u \cdot v= {uv}’ + {vu}’ \end{align}
\begin{align} u= \frac{1}{2} \tan x \end{align}
\begin{align} u’ = \frac{1}{2} \sec^{2} x \end{align}
\begin{align} v= {sen} ( 2x ) \end{align}
\begin{align} v’ =2 \cos ( 2x ) \end{align}
\begin{align} y’ = \frac{1}{2} \tan x \cdot ( 2 \cos ( 2x ) ) + \left[ {sen} ( 2x
) \cdot \frac{1}{2} \sec^{2} x \right] \end{align}
\begin{align} y’ = \tan x \cdot ( \cos ( 2x ) ) + \left[ {sen} ( 2x ) \cdot
\frac{1}{2} \sec^{2} x \right] \end{align}
\begin{align} y’ = \frac{{sen} x}{\cos x} \cdot ( 2 \cos^{2} ( x ) -1 ) +
\frac{1}{2} \left[ 2 {sen} ( x ) \cos ( x ) \cdot \frac{1}{\cos^{2} (
x )} \right] \end{align}
\begin{align}y’ = \frac{2 {sen} x \cos^{2} ( x )}{\cos x} – \frac{{sen}
x}{\cos x} + \frac{{sen} x \cos x}{\cos^{2} ( x )} \end{align}
\begin{align} y’ =2 {sen} x \cos x \end{align}
\begin{align} y’ = {sen} ( 2x ) \end{align}
\begin{align}5. y= – \frac{1}{4} \cos ( 4x ) + \frac{1}{12} \cos^{3} ( 4x ) \end{align}
\begin{align} y= – \frac{1}{4} \cos ( 4x ) + \frac{1}{12} [ \cos^{} ( 4x ) ]^{3} \end{align}
\begin{align} y’ = – \frac{1}{4} ( – {sen} ( 4x ) ) \cdot 4+ \left[ \frac{1}{4} (\cos ( 4x ) )^{2} \cdot ( – {sen} ( 4x ) ) \cdot 4 \right] \end{align}
\begin{align} y’ = {sen} ( 4x ) + [ \cos^{2} ( 4x ) \cdot ( – {sen} ( 4x ) ) ]\end{align}
\begin{align} y’ = {sen} ( 4x ) + [ 1- {sen}^{2} ( 4x ) \cdot ( – {sen} (4x ) ) ] \end{align}
\begin{align} y’ = {sen} ( 4x ) + [ – {sen}^{} ( 4x ) + {sen}^{3} ( 4x )] \end{align}
\begin{align} y’ = {sen} ( 4x ) – {sen}^{} ( 4x ) + {sen}^{3} ( 4x ) \end{align}
\begin{align}y’ = {sen}^{3} ( 4x )\end{align}
\begin{align} 6. y= x^{2} {sen} ( x ) +2x \cos ( x ) -2 {sen} ( x ) \end{align}
\begin{align}y’ = x^{2} [ \cos ( x ) \cdot 1 ] + {sen} ( x ) \cdot ( 2x ) +2x [ – {sen} ( x ) \cdot 1 ] + \cos ( x ) \cdot ( 2 ) -2 \cos ( x )
\end{align}
\begin{align} y’ = x^{2} \cos ( x ) +2x {sen} ( x ) -2x {sen} ( x ) +2\cos ( x ) -2 \cos ( x ) \end{align}
\begin{align} y’ = x^{2} \cos ( x ) \end{align}
\begin{align} 7 . y= \frac{1- {sen} ( x )}{1+ {sen} ( x )} \end{align}
\begin{align} \frac{u}{v} =v \frac{u’ – {uv}’}{v^{2}} \end{align}
\begin{align} u=1- {sen} ( x ) \end{align}
\begin{align} u’ =- \cos ( x )\end{align}
\begin{align} v=1+ {sen} ( x ) \end{align}
\begin{align}v’ = \cos ( x ) \end{align}
\begin{align} y’ = \frac{[ 1+ {sen} ( x ) ] [ – \cos ( x ) ] – [ 1- {sen} ( x )] [ \cos ( x ) ]}{[ 1- {sen} ( x ) ]^{2}} \end{align}
\begin{align}y’ = \frac{- \cos ( x ) – {sen} ( x ) \cos ( x ) – \cos ( x ) +{sen} ( x ) \cos ( x )}{[ 1- {sen} ( x ) ]^{2}}\end{align}
\begin{align} v’ = \frac{-2 \cos ( x )}{[ 1- {sen} ( x ) ]^{2}} \end{align}
Espero hayas podido resolver todos los ejercicios, si no no te preocupes solo sigue practicando!