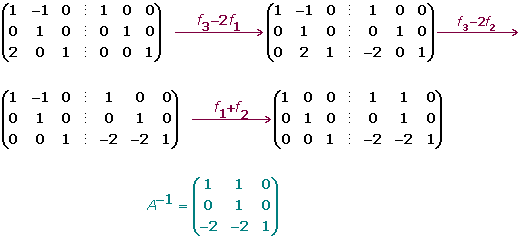Para obtener la Matriz Inversa de una Matriz es necesario que se cumplan ciertas condiciones.
Las condiciones para calcular la inversa de una matriz son las siguientes:
- Tiene que ser una matriz cuadrada
- Sea A una matriz su inversa es A^-1
- A^-1 x A = I e I=Matriz Identidad, es decir, matriz con unos en su diagonal principal y ceros todos los demás.
I = [1 0 0 … 0]
[0 1 0 … 0]
[0 0 1 … 0]
…
[0 0 0 … 1]
La manera de obtener A^-1 es haciendo Gauss-Jordan al arreglo [A | I]
Obteniendo: [I | A^-1]
Un ejemplo sencillo donde se puede apreciar es
- Teniendo A = [2 6]
[-3 4]
Encontrar la matriz inversa:
[2 6 | 1 0]
[-3 4 | 0 1]
Dividimos R1 entre 2
[1 3 | ½ 0]
[-3 4 | 0 1]
Ahora multiplicamos R1 por 3 y se lo sumamos a R2
[1 3 | ½ 0]
[0 13 | 3/2 1]
Dividimos R2 entre 13
[1 3 | ½ 0]
[0 1 | 3/26 1/13]
Ahora multiplicamos por -3R2 y le sumamos R1
[1 0 | 4/26 -3/13]
[0 1 | 3/26 1/13]
Entonces tenemos que:
A^-1 = [4/26 -3/13]
[3/26 1/13]
Para tener la matriz mas simple podemos simplificar factores y factorizarlos por un factor común y nos queda por último:
A^-1 = 1/26 * [4 -6]
[3 2]
Existe un manera par comprobar si la matriz resultante es la inversa de nuestra matriz original, esto consiste en multiplicar la matriz resultante por la matriz original y el resultado tiene que ser la matriz identidad.
Comprobamos:
1/26 * [4 -6] * [2 6]
[3 2] [-3 4]
= 1/26 [26 0] = [1 0]
[0 26] [0 1]
Por lo que estamos en lo correcto con nuestro resultado.
Este fue mas que nada un ejemplo sencillo para ir viendo el procedimiento a continuación un ejemplo un poco mas complejo pero que siguiendo los pasos es simple de resolver
- [-2 4 6]
[4 5 6]
[3 1 -2]
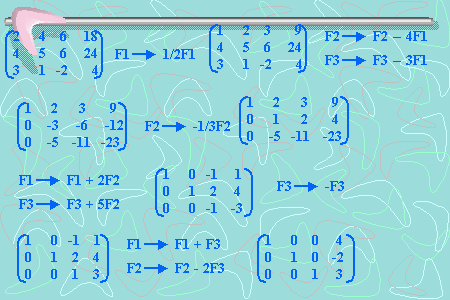
Empezamos poniendo en paralelo la matriz identidad a nuestra matriz original:
[2 4 6 | 1 0 0]
[4 5 6 | 0 1 0]
[3 1 -2 | 0 0 1]
Ahora empezamos con el Gaus-Jordan y dividimos R1 entre 2, nos queda:
[1 2 3 | ½ 0 0]
[4 5 6 | 0 1 0]
[3 1 -2 | 0 0 1]
Multiplicamos R1 por -4 y por -3 y le sumamos R2 y R3 respectivamente y nos queda:
[1 2 3 | ½ 0 0]
[0 -3 – 6 | -2 1 0]
[0 -5 -11 | -3/2 0 1]
Dividimos R2 entre -3
[1 2 3 | ½ 0 0]
[0 1 2 | 2/3 -1/3 0]
[0 -5 -11 | -3/2 0 1]
Ahora a R2 lo multiplicamos por 5 y le sumamos R3
[1 2 3 | ½ 0 0]
[0 1 2 | 2/3 -1/3 0]
[0 0 -1 | 11/6 -5/3 1]
Dividimos R3 entre -1
[1 2 3 | ½ 0 0]
[0 1 2 | 2/3 -1/3 0]
[0 0 1 | -11/6 5/3 -1]
Multiplicamos R3 por -2 y por -3 y sumamos R2 y R1 respectivamente
[1 2 0 | 6 -15/3 3]
[0 1 0 | 13/3 -11/3 2]
[0 0 1 | -11/6 5/3 -1]
Ahora multiplicamos por -2 R2 y le sumamos R1
[1 0 0 | -8/3 7/3 -1]
[0 1 0 | 13/3 -11/3 2]
[0 0 1 | -11/6 5/3 -1]
Por lo que nuestra matriz inversa es
A^-1 = [-8/3 7/3 -1]
[13/3 -11/3 2]
[-11/6 5/3 -1]
Para comprobarlo, lo multiplicamos por nuestra matriz original y obtenemos la matriz identidad sin mayor problema.
Algunos puntos importantes que no debemos de olvidar es cuidar bien nuestro álgebra para no cometer errores, lo demás es simplemente seguir bien el procedimiento de Gauss-Jordan.
Mas ejercicios:
1.
[1 -2 3]
[-2 2 7]
[-3 5 4]
2.
[3 2 1]
[0 2 2]
[0 0 1]