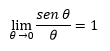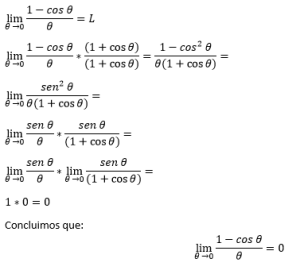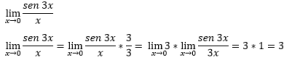Límites de funciones trigonométricas

Antes de estudiar los límites de funciones trigonométricas repasaremos brevemente el tema de funciones trigonométricas.

Funciones trigonométricas

Las funciones trigonométricas en el plano cartesiano se describen como relaciones entre los lados de un triángulo rectángulo (triángulo en el cual uno de sus ángulos es recto).

Si el triángulo tiene un ángulo agudo θ se pueden encontrar seis razones entre las longitudes de los lados a,b y c del triángulo:

b/c, a/c, b/a, a/b, c/a, c/b

Las relaciones son funciones de θ y se les llama funciones trigonométricas. Las funciones trigonométricas son: seno, coseno, tangente, cotangente, secante y cosecante, sus símbolos respectivamente son: sen, cos, tan, cot, sec y csc.

Si el ángulo θ es agudo a los lados del triángulo se les llama cateto adyacente, cateto opuesto e hipotenusa.

Es decir:

Sen θ = c. opuesto/hipotenusa

Cos θ = c. adyacente/hipotenusa

Tan θ = c. opuesto/c. adyacente

Cot θ = c. adyacente/c. opuesto

Sec θ = hipotenusa/c. adyacente

Csc θ = hipotenusa/c. opuesto

• Seno y cosecante son recíprocas entre sí.
• Coseno y secante son recíprocas entre sí.
• Tangente y cotangente son recíprocas entre sí.

Límites de funciones trigonométricas

Qué es un límite? Son los valores que toma una función dentro de un intervalo que se van aproximando a un punto fijo c. Se dice que el límite de la función f (x) es L cuando x tiende a c y se escribe:

Cuando calculamos límites de funciones trigonométricas es necesario recordar las siguientes identidades básicas:

1. Sen ² x + Cos ² x = 1
2. Tan x = Sen x/Cos x
3. Cot x = 1/tan x = Cos x/Sen x
4. Sec x = 1/Cos x
5. Csc x = 1/Sen x
6. Sen (α + β) = Sen α  Cos β + Cos α  Sen β
7. Sen (α – β) = Sen α  Cos β – Cos α  Sen β
8. Tan (α + β) = (Tan α + Tan β)/ 1 – Tan α Tan β
9. Tan (α – β) = (Tan α – Tan β)/ 1 + Tan α Tan β
10. Sen 2α = 2 Sen α Cos α
11. Cos 2α = Cos ² α – Sen ² α  = 2Cos ² α – 1 = 1 – Sen ² α
12. Tan 2α  = 2 Tan α / 1 – Tan ² α