 A menudo tropezarás con ejercicios que te desafían a saber ¿qué es el estudio de una función?. Te invito a redoblar la apuesta y aprender no sólo qué es sino cómo se hace el estudio de una función.
A menudo tropezarás con ejercicios que te desafían a saber ¿qué es el estudio de una función?. Te invito a redoblar la apuesta y aprender no sólo qué es sino cómo se hace el estudio de una función.
Antes de abordar el tema en sí mismo, te sugiero repasar algunos conceptos básicos sobre funciones en alguno de estos post anteriormente publicados:
- Concepto de función algebraica
- Dominio y codominio de una función algebraica
- Ejercicios de funciones
¿Qué es el estudio de una función?
Si me pides una definición sencilla, te diré que estudiar una función es poder determinar cómo se comportará gráficamente, sin necesidad de hacer una representación gráfica exhaustiva, punto por punto a partir de una tabla de valores.
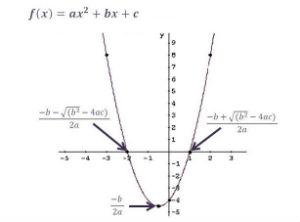
Lo que se hace al estudiar una función es determinar algunos aspectos claves como por ejemplo: pendiente (en el caso de las funciones lineales), concavidad (en el caso de las funciones cuadráticas), ordenada al origen (punto de corte con el eje vertical, de las “ordenadas” o de las “y” como se le llama habitualmente), raíz o raíces (dónde corta el eje horizontal o de las “absisas” o de las “x”) y vértice (en el caso de las funciones cuadráticas y otro tipo de curvas).
La propuesta de hoy es explicar cada uno de esos conceptos y determinar cómo se trabajan. En un próximo post, mediante un ejemplo haremos un estudio completo de una función lineal y un estudio completo de una función cuadrática.
- Pendiente
Se determina este parámetro sólo en el caso de las funciones lineales; se llama pendiente a la inclinación que tiene la recta que resulta de la representación gráfica de una función lineal, en relación al eje de las “x” u horizontal. Para determinarla, nos fijamos en el coeficiente de x en la expresión de la función, a saber si la expresión de la función fuera y= ax + b, sería:
- Si a > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje horizontal, es agudo.
- Si a < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.
En la siguiente imagen queda muy bien explicado:
- Concavidad
Sólo se determina en el caso de las funciones cuadráticas. Está determinada por el signo del coeficiente del término de segundo grado, que habitualmente llamamos a.
- Si a > 0 la función tiene concavidad positiva, y decimos que “sonríe” aludiendo a que la parábola que la representa parece una sonrisa (esto es un ayuda memoria que puede no gustar a tu profesor…, tenlo en cuenta).
- Si a < 0 la función tiene concavidad negativa y decimos que “está enojada” aludiendo a que la parábola parece una mueca de enojo.
- Ordenada al origen
Marca el punto de corte con el eje de las ordenadas o eje vertical. La hallas sustituyendo por 0 las x que veas en la expresión de la función, lo que comúnmente se conoce como “anular x”.
- Raíces o soluciones
Revelan el o los puntos de corte del gráfico de la función con el eje horizontal o de las abscisas. Se hallan convirtiendo la función en una ecuación y resolviéndola. Esa o esas soluciones -que podrían ser iguales entre sí o incluso no existir, son los puntos de corte que estás buscando.
- Vértice
Sólo se halla en el caso de las funciones cuadráticos. Representa el punto más “alto” de la curva si ésta tiene concavidad negativa (entonces decimos que es un máximo) o el punto más “bajo” si es una curva con concavidad positiva (entonces decimos que es un mínimo).
Al buscar el vértice lo que estás buscando es un punto, y por tato lo que buscas son sus coordenadas para ubicarlo en el plano. La coordenada x del vértice (se simboliza Vx) se halla con la fórmula Vx= -b /2a; la coordenada y se halla sustityuendo ése valor de Vx que hallaste antes, en cada lugar donde aparezca x en la expresión de la función; el resultado es la coordenada “y” del vértice.
Imagen: hpca2w13
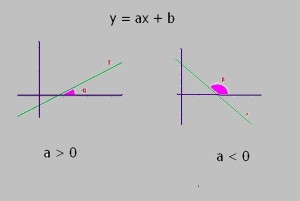

No hay respuetas