Tarde o temprano tu profesor te desafiará con este pedido: debes hacer el estudio de una función lineal. Hoy te enseño paso a paso cómo se hace con un ejemplo…
¿Qué es el estudio de una función? Abordamos este tema hace unos días, de modo que -para no repetir conceptos- te invito a leer ese post para que puedas contextualizar en forma adecuada el trabajo de hoy. El próximo post será complementario al de hoy, y tratará acerca del estudio de una función cuadrática. Pero sin más rodeos, te propongo ir al tema del título…
Estudio de una función lineal
Estudiar una función es poder determinar cómo se comportará gráficamente, sin necesidad de hacer una representación gráfica exhaustiva, punto por punto a partir de una tabla de valores.
En el caso del estudio de una función lineal, tenemos un esquema de trabajo muy claro que implica realizar en este orden el estudio de los siguientes ítems que explico brevemente:
Es la inclinación que tiene la recta que resulta de su representación gráfica, en relación al eje de las “x” Debes fijar atención en el coeficiente de x en la expresión de la función. Si la expresión de la función fuera y= ax + b, dirías que:
Si a > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje horizontal, es agudo.
Si a < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.
Determina el punto de corte con el eje vertical. Se halla sustituyendo por cero la x que ves en la expresión de la función, lo que comúnmente se conoce como “anular x”.
Revela el punto de corte del gráfico de la función con el eje horizontal. Se halla convirtiendo la función en una ecuación y resolviéndola.
En suma: l as funciones lineales son funciones de dominio real y
codominio real, cuya expresión analítica es
Ejemplo resuelto de estudio de función lineal
Vamos ahora a lo que estás esperando ansiosamente: un caso ejemplo resuelto, tal como te lo propondrían en un ejercicio de clase. Toma nota y vamos paso a paso:
Estudio de la función y=-3x+1
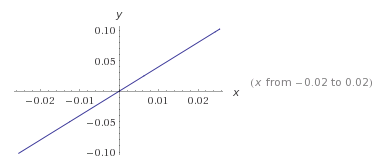
a=-3 ==> a<0 , ángulo obtuso respecto al eje horizontal, tal como lo muestra la siguiente figura:
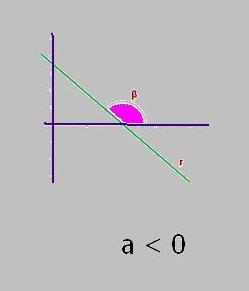
y = -3 x+1
y = -3 (0) + 1
y = 1
La ordenada al origen es 1, esto significa que la recta que representa gráficamente la función, corta el eje vertical en el punto y=1.
Como y= -3x + 1
La ecuación para esta función sería:
-3x + 1 = 0
-3x = -1
x= -1 / -3
x= 1/3
La raíz o solución es 1/3. Esto significa que la recta corta el eje horizontal o “de las x” en el punto x= 1/3.
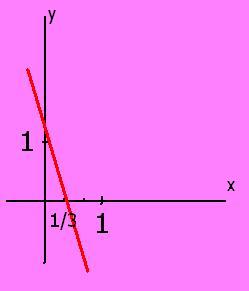
Así las cosas, el croquis correspondiente al estudio de la función dada quedaría de esta forma:
Te recuerdo que un croquis es exactamente eso: un dibujo que trata de respetar las proporciones lo mejor posible, pero no es gráficamente exacto ni mucho menos.
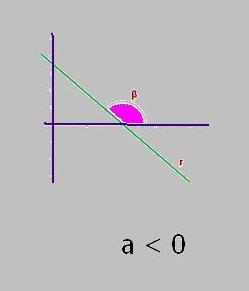
No hay respuetas