Las funciones logaritmicas y exponenciales están relacionadas ya que la función inversa de la función exponencial con base “a” se llama función logarítmica base “a” y se representa mediante loga (x) , se lee “logaritmo de x base a”.
Funciones logaritmicas y exponenciales
Definición de loga:
Sea “a” un número positivo real diferente a 1. El logaritmo de x con base “a” se define:
y = loga x solamente si x = ay (para toda “x” mayor a cero y todo número real “y”).
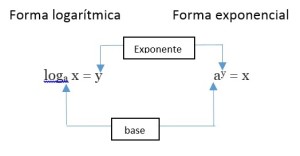
La primera ecuación es la forma logarítmica y la segunda es la forma exponencial, el siguiente diagrama puede ayudarte a convertir cada forma en la otra:
Ejemplos
log5 u =3 –> 53 = u
logb 3 =7 –> b7 = 3
log3 8 =3+2 –> 3(3+2) = 8
Funciones logarítmicas
Las siguientes son propiedades generales consecuencia de la interpretación de loga x como un exponente:
| Propiedad de Loga (x) | Motivo | Ejemplo |
|
|
|
Si a > 1 entonces loga x es creciente en (0, infinito).
Ejemplo
Hacer la gráfica para la función f(x) = log3 x :
Método 1
Ya que log3 x y 3x son inversas entre sí, primero se hace la gráfica de 3x , se refleja la recta y = x y el reflejo de la gráfica 3x será la gráfica de log3 x.
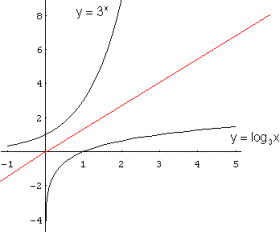
Método 2
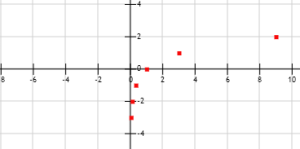
Determinar puntos en la gráfica de y = log3 x haciendo que x = 3k y aplicar la propiedad (3) de los logaritmos (del cuadro anterior), con esta fórmula obtenemos los siguientes puntos:
| x = 3k | 3-3 | 3-2 | 3-1 | 30 | 31 | 32 | 33 |
| y = log3 x = k | -3 | -3 | -1 | 0 | 1 | 2 | 3 |
Método 3
Se puede trazar la gráfica de y = log3 x graficando la forma exponencial x = 3y .
Funciones exponenciales
La función exponencial es de la forma f(x)= ax, siendo “a” un número real positivo.
Si tenemos f(x)= 3x, en la siguiente tabla aparecen algunas coordenadas de puntos de la gráfica de y =3x
|
X |
-10 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 10 |
| Y = 3x | 1/59049 | 1/27 | 1/9 | 1/3 | 1 | 3 | 9 | 27 |
59049 |
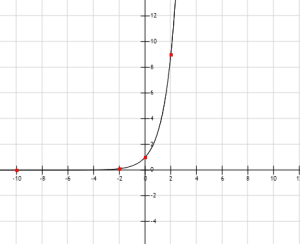
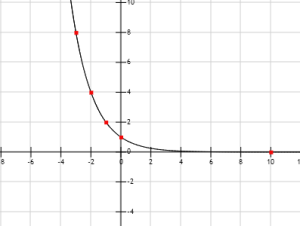
En la figura se ve el trazado de la gráfica de f(x)= 3x.
Si x1 y x2 son números racionales y x1<x2 entonces 3x1<3x2 y f es una función creciente y por lo tanto su gráfica es ascendente.
| Terminología | Definición | Gráfica de f para a > 1 | Gráfica de f para 0 < a < 1 |
| Función exponencial f con base “a” | f(x) = ax donde a es mayor a 0 y diferente a 1 | 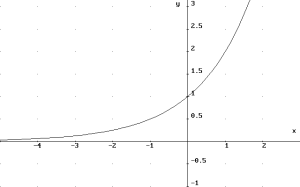 |
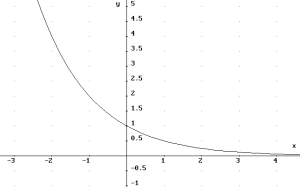 |
Si a > 1, entonces la función es creciente y si 0 < a < 1, la función es decreciente.
Ejemplos
1.- Tenemos la siguiente función F(x) = 3/2x
La siguiente tabla presenta las coordenadas de varios puntos en la gráfica
| X | -10 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 10 |
| Y = 3/2x | 10/59049 | 8/27 | 4/9 | 2/3 | 1 | 3/2 | 9/4 | 27/8 | 57.6 |
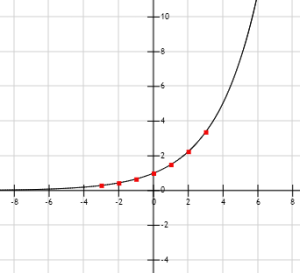
La gráfica es la siguiente:
La gráfica es creciente por que 3/2 es mayor a 1.
2.- Tenemos la siguiente función F(x) = 1/2x
La siguiente tabla presenta las coordenadas de varios puntos en la gráfica
| X | -10 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 10 |
| Y = 1/2x | 1024 | 8 | 4 | 2 | 1 | 1/2 | 1/4 | 1/8 | 1/1024 |
La gráfica es la siguiente:
La gráfica es decreciente por que 1/2 es menor a 1.
APLICACIONES
Las funciones exponenciales se presentan en muchos fenómenos, tiene tres aplicaciones:
- El crecimiento población
- La desintegración radioactiva
- El interés compuesto
En todos estos casos la variable es el tiempo.