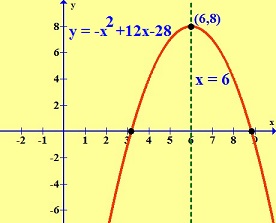
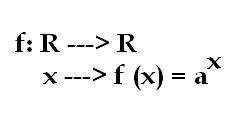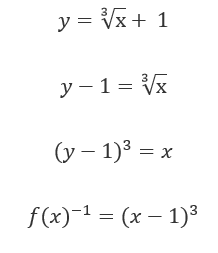Estudio de una función de segundo grado

Artículo previo Siguiente artículo

Llega el momento de abordar el estudio de una función de segundo grado, luego de haber trabajado sobre el estudio de una función lineal. Como siempre, te enseño paso a paso cómo se hace con un ejemplo…

Como paso previo, te invito a repasar los conceptos claves que compartimos en ocasión de responder la pregunta ¿Qué es el estudio de una función? . Ahora sí vamos al tema de hoy…

Estudio de una función de segundo grado

Como sabemos – pero vale la pena partir del concepto clave- , estudiar una función es poder determinar cómo se comportará gráficamente, sin necesidad de hacer una representación gráfica exhaustiva, punto por punto a partir de una tabla de valores.

En el caso del estudio de una función de segundo grado (también llamada cuadrática), tenemos un esquema de trabajo muy claro que implica realizar en este orden, el estudio de los siguientes ítems que te explico en forma sintética:

Concavidad

En palabras sencillas es determinar cómo será la curvatura de la parábola. Se condiciona a saber el signo del coeficiente del término de segundo grado, que habitualmente llamamos a.

Si a > 0 la función tiene concavidad positiva, y decimos que “sonríe” aludiendo a que la parábola que la representa parece una sonrisa (esto es un ayuda memoria que puede no gustar a tu profesor…, tenlo en cuenta).

Si a < 0 la función tiene concavidad negativa y decimos que “está enojada” aludiendo a que la parábola parece una mueca de enojo.

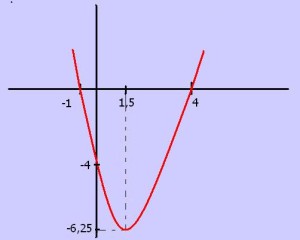
La siguiente imagen nos ilustra un caso de concavidad positiva:

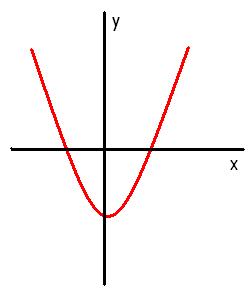
Ordenada al origen

Al calcular la ordenada al origen, estamos señalando el punto de corte con el eje de las ordenadas o eje vertical. La encuentras sustituyendo por 0 (cero) las x que veas en la expresión de la función, lo que comúnmente se conoce como “anular x”.

Raíces o soluciones

Revelan el o los puntos de corte del gráfico de la función con el eje horizontal o de las abscisas. Las calculas convirtiendo la función en una ecuación (igualándola a cero) y resolviéndola. Esa o esas soluciones -que podrían ser iguales entre sí o incluso no existir, son los puntos de corte que estás buscando.

Vértice

Representa el punto más “alto” de la curva si ésta tiene concavidad negativa (entonces decimos que es un máximo) o el punto más “bajo” si es una curva con concavidad positiva (entonces decimos que es un mínimo).

Al buscar el vértice lo que estás buscando es un punto, y por tato lo que buscas son sus coordenadas para ubicarlo en el plano. La coordenada x del vértice (se simboliza Vx) se halla con la fórmula Vx= -b /2a; la coordenada y se halla sustityuendo ése valor de Vx que hallaste antes, en cada lugar donde aparezca x en la expresión de la función; el resultado es la coordenada “y” del vértice.