Antes de abordar el tema de función exponencial, es importante tener claro qué es un exponente, porque un concepto está íntimamente ligado con el otro. Precisamente por ello, dedicamos un post antes a ese tema, con el fin de avanzar paso a paso de modo de clarificar el terreno para abordar hoy el tema que nos ocupa:
Función exponencial
Hablamos de función exponencial, si se cumple que existe una base a, que pertenece al conjunto de los números reales positivos, y sea distinta de 1, elevada a una variable x.
Lo antes dicho puede expresarse de la siguiente manera:
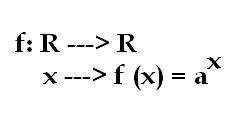 Esto se lee como función exponencial de base a, en “x”. Para comenzar a analizarla es recomendable recordar algunas propiedades de la potenciación, enfocando atención precisamente a los exponentes. Toma nota antes de seguir adelante:
Esto se lee como función exponencial de base a, en “x”. Para comenzar a analizarla es recomendable recordar algunas propiedades de la potenciación, enfocando atención precisamente a los exponentes. Toma nota antes de seguir adelante:
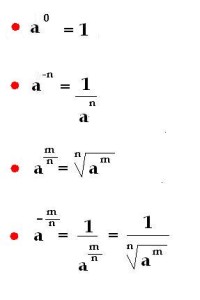
- Cualquier potencia de exponente 0, es igual a 1 (siempre que su base no sea 0)
- Cualquier potencia de exponente 1, es igual a la base.
Cero elevado a cualquier exponente (distinto de cero) es igual a cero. - Si la base de la potencia es un número positivo, el resultado siempre será positivo.
- Si la base de la potencia es un número negativo, el signo del resultado depende del tipo de exponente, a saber: si el exponente es par, el signo será positivo, pero si es impar, el exponente será negativo. Es importante ampliar este punto.
A estas propiedades, es importante sumar las siguientes, expresadas mejor a través de las siguientes igualdades, acerca de las que te recomiendo tomar nota y aprenderlas de memora (o tenerlas siempre a mano). Son cuatro:
Crecimiento de la función exponencial
Como bien sabemos, un atributo de las funciones matemáticas (entre ellas, desde luego, la función exponencial) es lo que se llama su crecimiento. Cuando realizamos el estudio de una función, se determina cuándo ésta es creciente o decreciente. En el caso de algunas funciones más complejas, esta es una condición que puede variar, por lo que deben determinarse intervalos de crecimiento, es decir cuándo la función se comporta como función creciente y cuándo no.
Pero en el caso que nos ocupa, vale decir la función exponencial, las condiciones de crecimiento o decrecimiento son muy claras; toma nota:
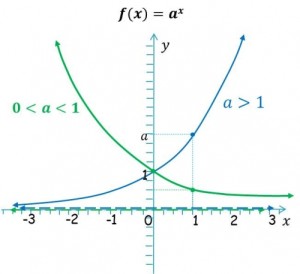
- a>1 En el caso de que la función exponencial tenga una base mayor que 1, se dice que esta función exponencial es estrictamente creciente en su dominio.
- a<1 En el caso en que la función exponencial de base a, sea menor que 1, se dice que esa función es estrictamente decreciente en su dominio.
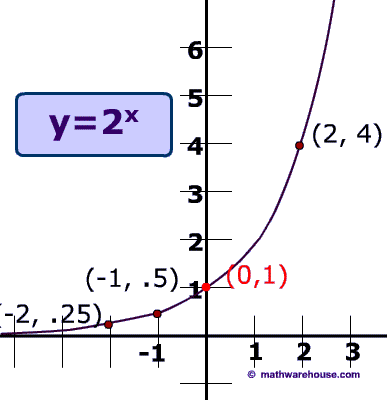
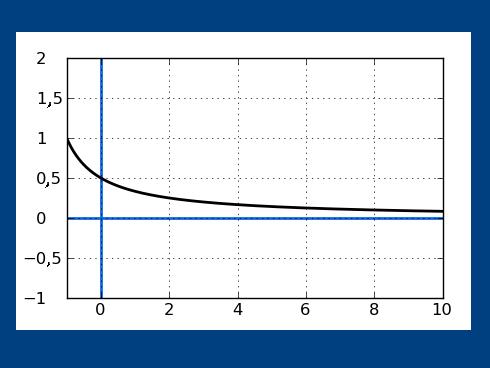
Lo antes señalado, puede verse con mayor claridad en las representaciones gráficas de cada tipo de función. En la siguiente imagen, mostramos la gráfica típica de una función exponencial sencilla (lo que varía en estos casos es la amplitud o concavidad de la curva en cuestión, pero en líneas generales la gráfica siempre es más o menos así)
En otro orden, cuando hablamos de una función exponencial decreciente, su curva será idéntica a la anterior pero simétrica respecto al eje “y” o vertical. Para que este concepto quede más claro, aquí compartimos una nueva imagen donde se observan ambos tipos de funciones, una creciente y una decreciente.