 Llegó el momento de profundizar en el tema, trabajando con algunos ejemplos de función exponencial. Paso a paso iremos analizando los mismos para que puedas llegar a dominar el tema y cuando te enfrentes a una función exponencial, sepas reconocerla y mejor aún, sepas qué hacer.
Llegó el momento de profundizar en el tema, trabajando con algunos ejemplos de función exponencial. Paso a paso iremos analizando los mismos para que puedas llegar a dominar el tema y cuando te enfrentes a una función exponencial, sepas reconocerla y mejor aún, sepas qué hacer.
Ejemplos de función exponencial
Antes de comenzar con los ejemplos propiamente dichos, repasaremos el concepto básico para que puedas distinguir cuándo una función es exponencial.
Te invito a observar los siguientes dos ejemplos de funciones:
f(x) = x2 y g(x) = 2x
Observa atentamente: ambas funciones se parecen pero definitivamente no son iguales. En el caso de la función f(x) = x2 se observa claramente que hablamos de una función cuya variable “x” está elevada a un exponente numérico. Es fácil determinar que es una simple función cuadrática de un solo término.
Pero te invito a mirar ahora con atención la otra función del ejemplo; en este caso hablamos de la función g(x) = 2x , que tiene una sutil pero importante diferencia con la anterior. Esta función, tiene una base numérica (en este caso 2) y un exponente que es una variable.
Precisamente, cuando la variable de una función es un exponente, es que estamos en presencia de una función exponencial.
¿Cómo se define una función exponencial?
Una función exponencial con base a es una función de la forma f(x) = ax , donde a y x son números reales tal que a> 0 y a es diferente de uno. Es interesante (y pertinente) definir que el dominio de este tipo de funciones, es el conjunto de números reales y el codominio será el conjunto de todos los números reales positivos.
¿Una función exponencial puede tener entonces exponente negativo? Pues sí. Si analizamos cuáles son las condicionantes que planteamos al definirla, acerca de x sólo hemos dicho que debe pertenecer a los números reales, por lo que un entero negativo entra perfectamente en el cumplimiento de estas condiciones.
Por ejemplo, menciono a la función
f(x) = 2-x
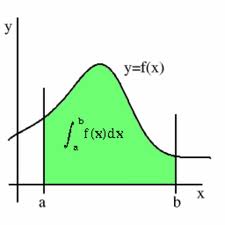
Lo que sucederá en este caso, es que no tendrá un crecimiento exponencial, sino precisamente lo contrario: un decrecimiento exponencial. Su gráfica podría ser algo como la siguiente imagen:
Veamos ahora algunas de las propiedades más importantes de este tipo de funciones.
Propiedades de las funciones exponenciales
Definiendo a nuestra función exponencial como la siguiente (a los efectos de la enunciación de las propiedades)
f(x) = ax, a>0, a distinto de 1
Decimos que…
1) Su gráfica siempre pasa por el punto (0,1).
2) Su representación gráfica es siempre continua, es decir no tiene puntos de corte.
3) La función tiene una asíntota horizontal, que es el propio eje de las “x” o eje de las abscisas. Para refrescar el concepto, te invito a releer el post ¿Qué es una asíntota?
4) Si se da el caso que a> 1 (a, es la base), entonces ax aumenta a medida que aumenta x.
5) Si se da el caso que 0 < a < 1, entonces ax disminuirá a medida que aumenta x.
6) Este tipo de funciones es del tipo “uno a uno”.
- Caso especial de función exponencial
Te lo encontrarás varias veces por lo que vale la pena mencionar este caso especial. Hablamos del momento en que la base de la función es el famoso “número e”.
Por si no lo sabes, e es un número irracional cuyo valor se define como e = 2.71828… Se llama e, porque así lo “bautizó” el matemático Leonhard Euler (1727).
Una función exponencial de base “e”, tiene una estructura como la siguiente:
f(x) = ex
A tal punro es importante que si observas con atención verás que las calculadoras científicas poseen una tecla especial para este tipo de función f(x) = ex. Su gráfica luce como la imagen de portada de este mismo post.