¿Cuáles son las funciones trigonométricas recíprocas? ¿Qué son las funciones trigonométricas?
Las funciones trigonométricas son razones trigonométricas, es decir la división entre dos lados de un triángulo rectángulo respecto a sus ángulos, estas funciones surgieron al estudiar el triángulo rectángulo y observar que los cocientes entre las longitudes de dos de sus lados sólo dependen del valor de los ángulos del triángulo.
Las funciones trigonométricas tienen varias aplicaciones en astronomía, matemáticas, física, en planos y en algunos otros fenómenos.
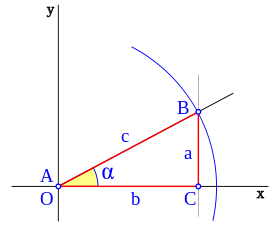
Para definir las funciones trigonométricas del ángulo: 
, del vértice A, se parte de un triángulo rectángulo. El nombre de los lados de este triángulo rectángulo son:
- La hipotenusa (c) es el lado opuesto al ángulo recto, o el lado más grande.
- El cateto opuesto (a) es el lado opuesto al ángulo .
- El cateto adyacente (b) es el lado adyacente al ángulo .
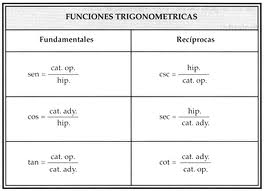
Existen tres funciones trigonométricas fundamentales: seno, coseno y tangente, y tres funciones trigonométricas recíprocas: cosecante, secante y cotangente.
Funciones trigonométricas recíprocas
1) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:
cot α = adyacente/opuesto
La función cotangente es recíproca de la función tangente.
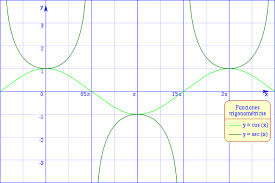
2) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:
sec α = hipotenusa/adyacente
La función secante es recíproca de la función coseno.
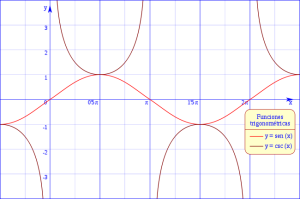
3) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:
csc α = hipotenusa/opuesto
La función cosecante es recíproca de la función sen.
Identidades trigonométricas: Recíprocos
\begin{align} {sen} ( A ) = \frac{1}{\csc ( A )} \csc ( A ) =\frac{1}{{sen} ( A )} \cos ( A ) = \frac{1}{\sec ( A )} \end{align}
\begin{align} sec ( A ) = \frac{1}{\cos ( A )} \tan ( A ) = \frac{1}{\cot ( A )} \cot ( A ) = \frac{1}{\tan ( A )}\end{align}
